Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 66
66. Determine o local e do ponto de aplicação força de modo que a tração desenvolvida nos cabos , e seja a mesma. Despreze o peso da chapa.
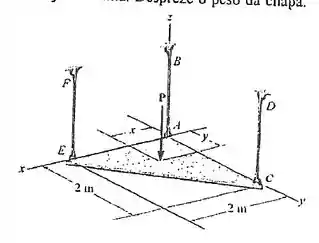
Passo 1
Fala! A gente quer posicionar de modo as trações nas cordas sendo iguais.
Então a gente precisa achar e , as coordenadas do ponto onde é aplicada.
Primeiro temos que avaliar que tipos de conexões temos nessa situação, nesse caso são cabos e segundo a tabela do capítulo , seção , esse tipo de conexão só exerce uma força ou tração na direção do cabo.
Para facilitar nossa vida, vamos estabelecer eixos coordenados novos que tenham sua origem no ponto onde a força atua, pois assim ela não contribui para o cálculo do momento referente a esses eixos novos. Abaixo há um diagrama de forças que ilustra essa ideia.
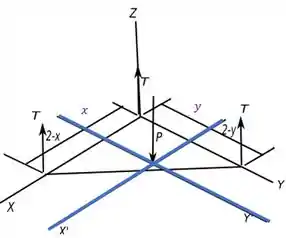
Tendo isso em mente, podemos determinar que satisfaça a condição do enunciado, usando as equações de equilíbrio para o momento referente aos novos eixos.
Passo 2
Agora vamos usar a equação de equilíbrio do momento em relação a .
Aqui os braços de alavanca vão ser retirados do eixo . Aí a gente procura nesse eixo a distância entre as coordenadas de (que a gente colocou como sendo a origem no novo sistema) até a coordenada da aplicação dos .
Momentos em sentidos opostos ficam com sinais opostos. Temos então
Passo 3
Agora vamos usar a equação de equilíbrio do momento em relação a .
Aqui os braços de alavanca vão ser retirados do eixo . Aí a gente procura nesse eixo a distância entre as coordenadas de (que a gente colocou como sendo a origem no novo sistema) até a coordenada da aplicação dos .