Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 73
73. Determine as componentes de força atuando na junta esférica em , a reação no rolete e a tração na corda , necessários para o equilíbrio da placa de um quarto de círculo.
Passo 1
Primeiro temos que avaliar que tipos de conexões temos nessa situação, nesse caso é uma corda, uma junta esférica e um rolete, segundo a tabela do capítulo , seção , esse tipo de conexão por corda só exerce uma força ou tração na direção do cabo, a junta esférica exerce força nas três direções dos eixos coordenados e o rolete só exerce força na direção vertical.
Abaixo temos um diagrama de corpo livre que mostra nossa situação.
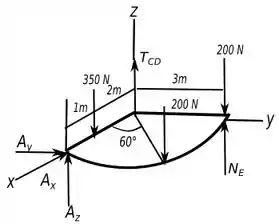
Passo 2
Primeiro vamos utilizar as equações de equilíbrio que nos dão o menor número de incógnitas, então vamos analisar a equação de equilíbrio em relação ao momento nos eixos e e depois da força em relação aos mesmos eixos.
Para a equação de equilíbrio referente ao momento temos que saber a distância que a força de faz com esses eixos, mas isso é fácil, basta decompor a distância que essa força tem da origem em suas componentes e , como temos o ângulo isso fica fácil, assim temos as distancias que precisamos.
Logo:
Passo 3
Agora para achar que é a única que falta, basta usar a equação de equilíbrio referente a força em relação ao eixo .