Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 115
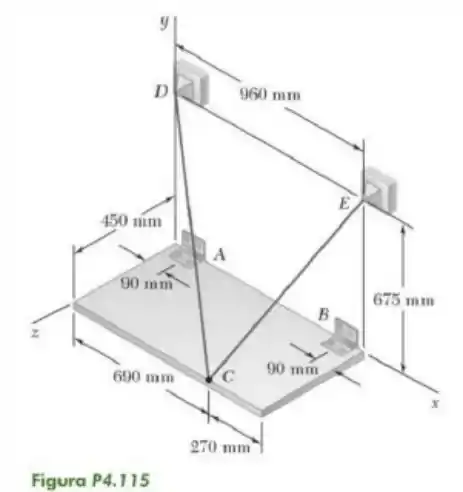
115- Uma placa retangular uniforme de de massa é sustentada na posição mostrada na figura pelas dobradiças e e pelo cabo , que passa por uma gancho sem atrito em . Considerando que a tração é a mesma em ambas as partes do cabo, determine a tração no cabo, as reações em e . Considere que a dobradiça em não exerce qualquer esforço axial.
Passo 1
O enunciado nos diz que não há nenhuma força de reação igual a o que faz com que o sistema de forças na placa seja:
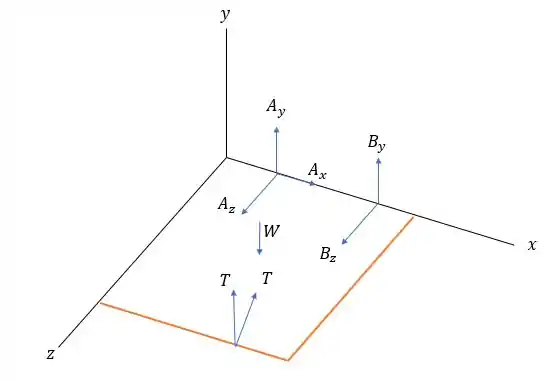
Onde é o peso da placa e vale:
Ou de modo vetorial:
E está na posição de:
E a vetorização das forças nos cabos e valem:
Passo 2
Agora vamos pegar essas forças todas e fazer a somatória dos momentos no eixo para encontrar o módulo da força :
Onde a distância relativa das forças ao eixo é apenas a distância no eixo (Considerando as forças saindo de ). Fazendo essas determinantes temos:
Isso nos dá:
Passo 3
Agora vamos fazer a somatória dos momentos em :
Agora as distâncias relativas são em relação a isso fará com que as determinantes valham:
Fazendo a somatória dos elementos que tem nós teremos:
Agora fazendo a somatória dos elementos que tem :
Isso faz com que a reação em seja:
Passo 4
Agora fazendo a somatória de todas as forças temos a força em :
Dessa forma:
Juntando os termos temos:
Isso faz com que a reação em seja: