Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas fundamentais - Ex. 7
6.7 Determine a força nos membros BC, CF e FE. Indique se os membros estão sob tração ou compressão.
Passo 1
Precisamos usar o método das seções para descobrir a força nos membros BC, CE e FE. Então vamos seccionar essa treliça onde temos esses três membro:
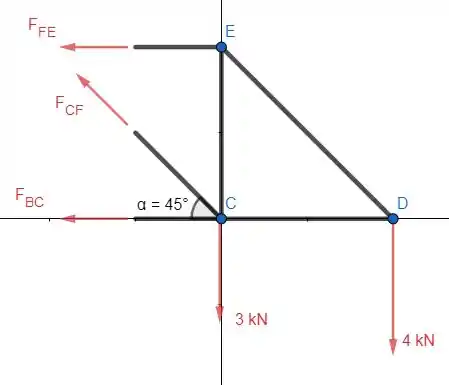
A treliça deve permanecer parada, então vamos fazer o somatório das forças em e em
Passo 2
Vamos analisar a equação em :
Multiplicando por :
Passo 3
Vamos analisar o eixo :
Como o resultado dessa força é positiva o sentido adotado para ela está correto. Além disso como essa força “puxa” o membro CF podemos dizer que ele está sob tração. Podemos escrever:
Passo 4
Podemos escolher qualquer ponto para calcular o momento, pois em todos eles o momento será igual a zero. Então vamos escolher o ponto C, pois existem 3 forças passando por ele, ou seja, que não geram momento
Da mesma forma que em CF essa força foi adotada no sentido correto e é uma força que está tracionando o membro. Podemos escrever:
Passo 5
Agora vamos resolver a equção que encontramos no passo 2, pois já temos os valores de e :
Diferente das forças e essa força foi assumida na direção errada, dessa forma ela não está “puxando”, mas “empurrando” a barra. Então BC está sofrendo compressão. Podemos escrever: