Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 134
O mecanismo de duas barras consiste de uma alavanca e uma barra lisa , que possui um colar liso fixo em sua extremidade e um rolete na outra ponta . Determine a força necessária para manter a alavanca na posição . A mola possui uma rigidez e um comprimento não estendido de . O rolete está em contato com a parte superior ou a inferior da guia horizontal.
Passo 1
Para determinar a força , deve-se fazer o diagrama de corpo livre de cada membro no qual sejam indicadas todas as forças atuando no respectivo membro. A partir dos DCLs será possível montar equações de equilíbrio para cada membro analisado.
Além disso, é possível fazer uma análise prévia sobre a força da mola. Deve-se lembrar que a mola comprime, ou seja, varia o seu comprimento de que, nesse caso, é dado por:
Dessa forma, a força elástica da mola dada pela Lei de Hooke será dada como:
Passo 2
Então, fazendo o DCL do membro e fazendo a análise das forças em , tem-se que:
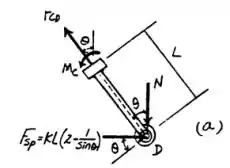
E para o momento em relação a :
Passo 3
Analogamente, será feita a análise do membro através de seu DCL e montando as equações de equilíbrio necessárias.
Então, a partir do seu DCL:
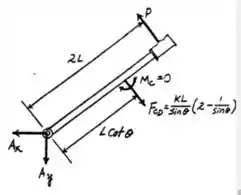
E aplicando o princípio dos momentos em relação ao ponto e supondo que o momento é positivo no sentido anti-horário, tem-se que:
Lembrando que e :
Portanto,