Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 135
Determine as componentes horizontal e vertical da reação nos apoios pinados e da montagem de vigas compostas.
Passo 1
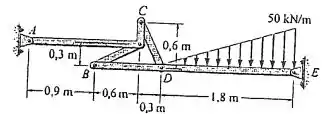
Para determinar as reações em cada pino, deve-se fazer o diagrama de corpo livre de alguns membros do corpo todo no qual sejam indicadas todas as forças atuando no respectivo membro. Para tanto, será feita a análise dos membros e visto que ambos possuem elos de ligação em comum.
Além disso, como o membro possui uma carga distribuída, se torna necessário determinar a força resultante gerada por essa carga e o ponto de aplicação da mesma.
Visto que a carga é triangular, a força resultante se dará por:
E o seu ponto de aplicação, a partir do ponto será de:
Passo 2
Então, fazendo o DCL do membro e fazendo a análise de momento em relação ao ponto , considerando que o momento é positivo no sentido anti-horário, tem-se que:
Passo 3
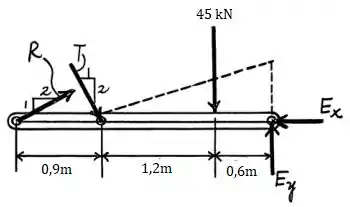
Agora, fazendo o DCL do membro e fazendo a análise de momento em relação ao ponto , considerando que o momento é positivo no sentido anti-horário, tem-se que:
Passo 4
A partir das equações (1) e (2), as forças nos elos de ligação serão a solução de tal sistema de equações e serão dadas por:
Passo 5
Com esses dois valores encontrados é possível retornar à análise dos membros e verificar os equilíbrios de força em cada eixo a fim de determinar as reações restantes.
Sendo assim, para o eixo do membro :
E para o eixo do membro , tem-se que:
Passo 6
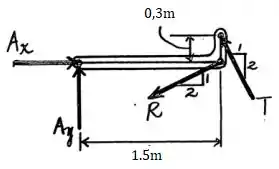
Analogamente, fazemos o mesmo processo com o membro para determinar as reações em .
Então, analisando o eixo do membro :
E, por fim, para o eixo do membro , tem-se que: