Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 68
68. Determine a intensidade da força que precisa ser exercida sobre o cabo da manivela em para manter a caixa de na posição mostrada. Além disso, determine as componentes da reação no mancal axial e no mancal radial liso .
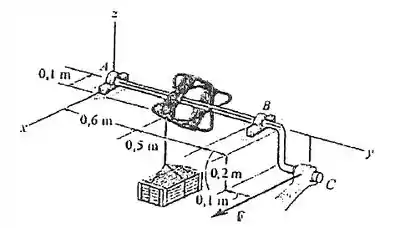
Passo 1
Queremos o valor de , e das reações em e .
Primeiro temos que avaliar que tipos de conexões temos nessa situação, nesse caso são dois mancais, um axial e o outro radial liso e segundo a tabela do capítulo , seção , o mancal axial exerce força nas três direções e o radial só em duas direções.
Para achar essas forças teremos que fazer um truque, para achar as componentes do mancal axial vamos definir novos eixos coordenados com origem no mancal radial, pois com os eixos já existentes não poderíamos calcular momentos onde as componentes do mancal axial aparecessem e se só usássemos as equações de equilíbrio da força, teríamos mais incógnitas do que equações.
Temos que saber também qual a força exercida pela caixa sobre o carrinho, mas isso é fácil, já que essa força vai ser igual a força peso da caixa que é dada por:
Onde é a massa do objeto e é a aceleração da gravidade. Logo a força peso do carrinho é:
Abaixo tem um diagrama de força que mostra a situação.
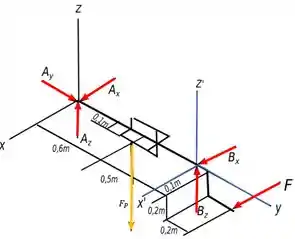
Passo 2
Primeiro, vamos calcular o que conseguimos com os eixos originais. É importante em cada eixo que formos observar, você passar por cada forcinha e se perguntar se ela gera momento naquele eixo, beleza?
Começando pelo somatório de momentos em . Vamos considerar como os momentos positivos os que tem sentido anti-horário olhando para . Então vamos lá:
Agora para , os positivos estão no sentido anti-horário olhando para o plano .
De forma análoga, vamos para o eixo :
Como só temos uma força que tem a mesma direção que o eixo , temos:
Passo 3
Agora, vamos calcular o que conseguimos com os novos eixos. A adoção de sinais vai ser parecida com o passo anterior. Então vamos lá:
Agora para :