Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 5.Problemas - Ex. 78

78. A placa possui um peso W com centro de gravidade em G . Determine a tração desenvolvida nos fios A B ,   C D e E F se a força P = 0,75 W é aplicada em d = L 2 .

Passo 1

Primeiro temos que avaliar que tipos de conexões temos nessa situação, nesse caso são três cabos, segundo a tabela 5.2 do capítulo 5 , seção 5.5 , esse tipo de conexão por cabo só exerce uma força ou tração na direção do cabo.

Para facilitar nossa vida em um momento, vamos definir novos eixos y ' e x ' , o eixo y ' passando pela força T E F e o eixo x ' passando pela força T E F e T C D , pois quando formos usar a equação de equilíbrio em relação a esses eixos, certas forças não contribuíram para o momento.

Abaixo temos um diagrama de corpo livre que vai nos ajudar a ver o que está acontecendo.

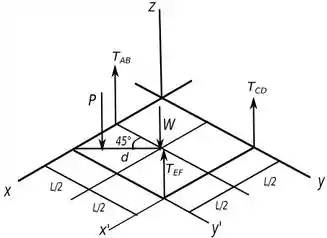
Agora só temos que aplicar as equações de equilíbrio para achar as forças que queremos.

O macete é sempre começar com as equações que te oferecem menos incógnitas.

Passo 2

Vamos começar com a equação do equilíbrio referente ao momento em relação ao eixo x ' , para obtermos T A B .

∑ M x ' = 0

0,75 W L 2 + L 2 cos ⁡ 45 ° + W L 2 - T A B L = 0

O termo L 2 cos ⁡ 45 ° é a distância L 2 projetada no eixo que passa por G que contribui para expressar a distância perpendicular de P ao eixo x ' , para o cálculo do momento.

⇒ 0,375 W L + 0,265 W L + 0,5 W L - L T A B = 0

⇒ 0,375 W + 0,265 W + 0,5 W - T A B = 0

⇒ T A B = 0,375 W + 0,265 W + 0,5 W

⇒ T A B = 1,14 W

Passo 3

Agora vamos analisar as equações de equilíbrio referente ao momento em relação aos eixos y e y ' .

∑ M y = 0

W L 2 + 0,75 W L 2 + L 2   s e n   45 ° - 1,14 W L 2 - T E F L = 0

O termo L 2   s e n   45 ° é a distância L 2 projetada no eixo x que contribui para expressar a distância perpendicular de P ao eixo y , para o cálculo do momento.

⇒ 0,5 W L + 0,375 W L + 0,265 W L - 0,57 W L - L T E F = 0

⇒ 0,5 W + 0,375 W + 0,265 W - 0,57 W - T E F = 0

⇒ T E F = 0,5 W + 0,375 W + 0,265 W - 0,57 W

T E F = 0,57 W

∑ M y ' = 0

T C D L + 1,14 W L 2 - W L 2 - 0,75 W L 2 - L 2   s e n   45 ° = 0

O termo L 2   s e n   45 ° é a distância L 2 projetada no eixo x que contribui para expressar a distância perpendicular de P ao eixo y ' , para o cálculo do momento.

⇒ L T C D + 0,57 W L - 0,5 W L - 0,375 W L + 0,265 W L = 0

⇒ T C D + 0,57 W - 0,5 W - 0,375 W + 0,265 W = 0

⇒ T C D - 0,04 W = 0

⇒ T C D = 0,04 W

Resposta

T A B = 1,14 W

T C D = 0,04 W

T E F = 0,57 W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o Problema 4.95 , considerando que o eixo foi girado no sentido horário em seus mancais de 30 ° e que a carga de 720N permanece na vertical.
A placa quadrada de peso 320N mostrada na figura é sustentada por três arames verticais. Determine a tração em cada arame.
A placa quadrada de peso 320N mostrada na figura é sustentada por três arames verticais. Determine o peso e a localização dos blocos mais leves que poderiam ser colocados na placa se a tração nos três
Dois tubos de aço A B e B C , cada qual com uma massa por unidade de comprimento de 8 k g / m , são soldados juntos em B e estão sustentados por três arames. Sabendo que a = 0,375m , determine a traçã
Para a montagem dos tubos do Problema 4.101 determine a o maior valor admissível de a para o conjunto não virar e b a correspondente tração em cada arame.