Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 14

7.14. Uma barra semicircular é carregada tal como mostra a figura. Determine a intensidade e a localização do momento fletor máximo na barra.

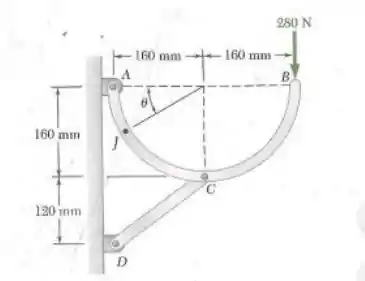
Passo 1

Vamos começar desenhando a situação

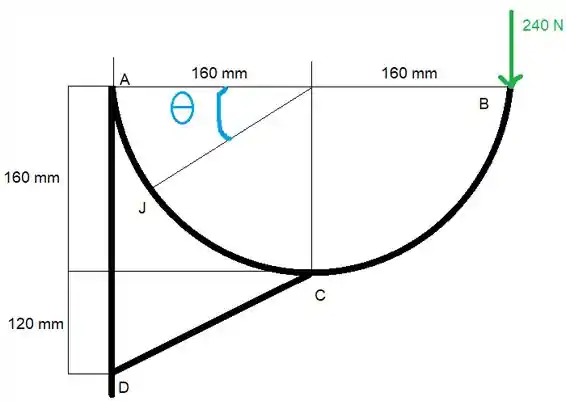
Então temos um semicírculo de raio 180   m m .

Aqui a gente já pode determinar a força F C D . Para isso vamos começar usando o momento em A. Mas a gente vai precisar decompor a força F C D nos eixos

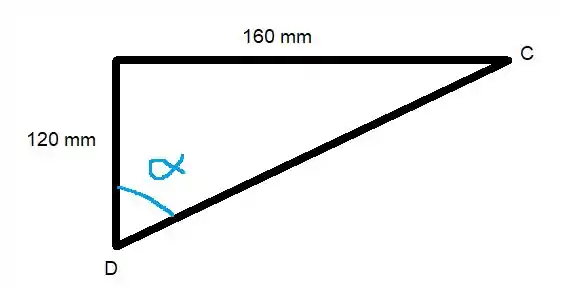
Vamos calcular a hipotenusa disso

h = 120 2 + 160 2 = 200

Então nós temos

F C D x = F C D ⋅ sin ⁡ α = F C D 160 200

E

F C D y = F C D ⋅ cos ⁡ α = F C D 120 200

Agora é só calcular o momento

∑ M A = 0

r 4 5 F C D + r 3 5 F C D - 2 r ⋅ 280 = 0

Mas pela imagem vemos que o raio é 160   m m , então só tem uma incógnita. Logo

F C D = 400   N

Outra coisa que podemos fazer é descobrir as forças de reação em A, para isso vamos usar as equações de equilíbrio de forças

∑ F x = 0

- A x + 4 5 ⋅ 400 = 0

Logo

A x = - 320   N

E agora em y

∑ F y = 0

A y + 3 5 ⋅ 400 - 280 = 0

Logo

A y = 40   N

Passo 2

Agora para achar as forças que precisamos a gente tem que usar o corpo livre em A J - para θ < 90 °

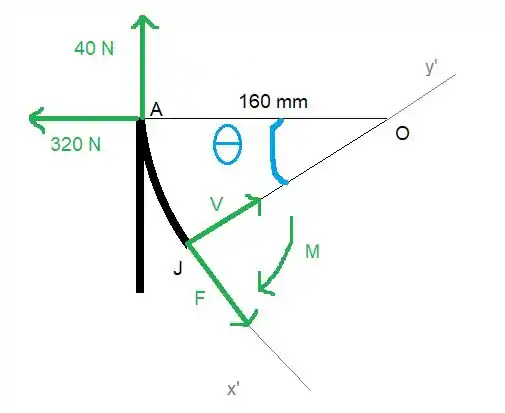
Agora para determinar o maior momento fletor vamos fazer

∑ M j = 0

320 ⋅ 0,16 ⋅ sin ⁡ θ - 40 ⋅ 0,16 ⋅ 1 - cos ⁡ θ - M = 0

Então

M = 51,2 sin ⁡ θ + 6,4 cos ⁡ θ - 6,4

Para o valor máximo, a gente usa aquele truque de calculo de derivar e igualar à 0

d M d θ = 0

Vamos fazer então

51,2 ⋅ c o s θ - 6,4 ⋅ sin ⁡ θ = 0

Vamos manipular isso

51,2 ⋅ c o s θ = 6,4 ⋅ sin ⁡ θ

Agora a gente divide tudo por cosseno

51,2 = 6,4 tan ⁡ θ

Agora isolando o θ

θ = arctan ⁡ 51,2 6,4 = 82,87 °

Agora que temos o valor de θ , vamos colocá-lo em M

M = 51,2 sin ⁡ ( 82,87 ° ) + 6,4 cos ⁡ ( 82,87 ° ) - 6,4

Logo

M = 45,2   N ⋅ m

E sua localização é θ = 82,87 °

Resposta

M = 45,2     N ⋅ m

θ = 82,87 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O arranjo composto da balança de bandeja é mostrado na figura. Se a massa sobre a bandeja é de 4 k g , determine as componentes horizontal e vertical nos pinos A , BeC , e a distância x da massa de 25
A caçamba de retroescavadeira e seu conteúdo possuem um peso de 6 k N e um centro de gravidade em G . Determine as forças do cilindro hidráulico A B e nas ligações A C e A D para manter o carregamento
Determine as reações no apoio fixo E e no apoio móvel A . O pino, conectado ao membro B D , atravessa um rasgo liso em D .
Um homem com peso de 875 N( ≈ 87,5 k g ) tenta se suspender usando um dos dois métodos mostrados. Determine a força total que ele precisa exercer na barra A B em cada caso e a reação normal que ele ex
Um homem com peso de 875 N( ≈ 87,5 k g ) tenta se suspender usando um dos dois métodos mostrados. Determine a força total que ele precisa exercer na barra A B em cada caso e a reação normal que ele ex