Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 136

Substitua o sistema de forças paralelas que age sobre a chapa por uma força resultante equivalente e especifique sua posição no plano x - z .

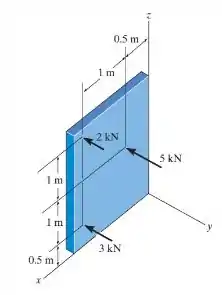
Passo 1

Desejamos encontrar a resultante equivalente de todas essas forças e, além disso, encontrar a posição de onde se encontra essa força no plano x - y . Sendo assim, temos

F r y = ∑ F y → F r = - 5 k N - 2 k N - 3 k N = - 10 k N

O sinal de negativo indica apenas que está do “lado” negativo do eixo y . Para encontrarmos a posição onde essa força está sendo aplicada vamos utilizar as equações do momento

M R x = ∑ M x  

→ 10 k N ⋅ z = 3 k N ⋅ 0,5 m + 5 k N ⋅ 1,5 m + 2 k N ⋅ 2,5 m

z = 1,40   m

M r z = ∑ M z

→   - 10 k N ⋅ X = - 5 k N ⋅ 0,5 m - 2 k N ⋅ 1 , , 5 m - 3 k N ⋅ 1,5 m

x = 1,00   m

Resposta

F r = - 10 k N ,   x = 1,0   m   e   z = 1,40   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

18. Determine o momento da força F em relação aos eixos x, y e z. Use uma análise escalar.
Determine o momento de binário resultante dos dois binários que agem sobre o encanamento. A distância de A a B é d = 400m m . Expresse o resultado como um vetor cartesiano.
Determine a distância d entre A e B tal que o momento de binário resultante tenha uma intensidade de M R = 20N ⋅ m .
Expresse o momento do binário agindo sobre a estrutura na forma de um vetor cartesiano. As forças são aplicadas perpendicularmente à estrutura. Qual é a intensidade do momento de binário? Considere F
Determine a intensidade das forças de binário F 1 e F 2 de modo que o momento de binário resultante que age sobre o bloco seja zero.