Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 21
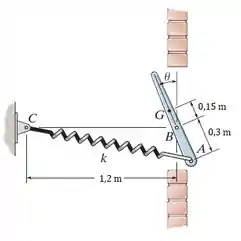
A placa de ventilação é apoiada em por um pino. Se ela pesa e tem um centro de gravidade em , determine a rigidez da mola de modo que a placa permaneça em equilíbrio em . A mola está livre quando .
Passo 1
Nosso sistema tem apenas um grau de liberdade, definido pela coordenada independente , beleza? Quando ocorre um deslocamento positivo , apenas a força elástica e o peso da placa de ventilação realizam trabalho!
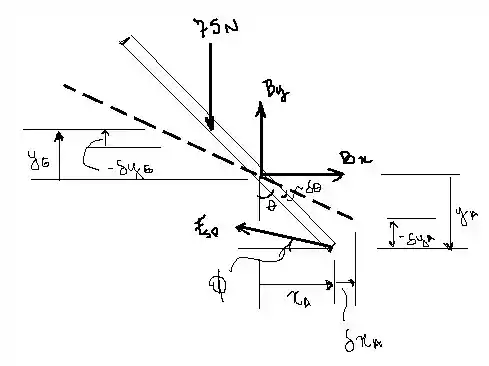
O peso da placa de ventilação está localizado em , distante do ponto na coordenada . As posições horizontal e vertical da força elástica são encontradas nas coordenadas e distantes do ponto , respectivamente. Assim, podemos escrever que:
Passo 2
Quando e fazem os deslocamento virtuais positivos e , o peso da placa, a componente horizontal de () e a componente vertical de () fazem trabalho negativo. Assim, se um corpo está em equilíbrio, a soma algébrica do trabalho virtual realizado por todas as forças e momentos de binário que atuam sobre o corpo é zero para qualquer deslocamento virtual do corpo.
Substituindo os valores de na equação acima, temos:
Como , temos:
Passo 3
No ponto de equilíbrio , o valor do ângulo pode ser encontrado através da tangente inversa, obtida pelo diagrama abaixo:
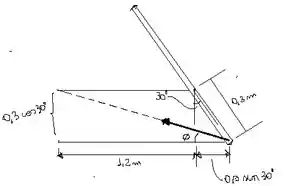
Assim, o valor de é igual a:
Passo 4
Para encontrarmos o valor de , vamos partir pela geometria plana. Aplicando a lei dos cossenos, temos a seguinte relação:
Aplicando a lei de Hooke, temos:
Resposta
A rigidez da mola é igual a: