Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 80
80. Usando o método da seção , resolva o problema .
Passo 1
Bom! A primeira coisa que vamos ter que fazer, é o diagrama de corpo livre da , onde estarão presentes três forças, que chamaremos de , e . As direções dessas forças se interceptarão em um ponto comum, que chamaremos de :
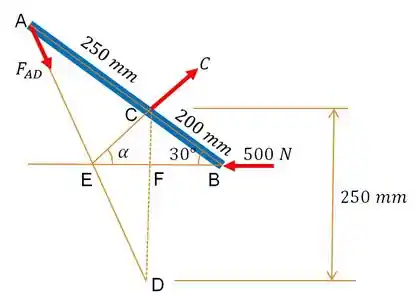
Agora; uma vez que o segmento na verdade é um prolongamento de ; consideraremos que é um triângulo isósceles e portanto:
E do triângulo , nós tiramos que o ângulo do triângulo vai ser dado pela soma dos ângulos opostos ao vértice e que são adjacentes, no caso e :
Consequentemente, como é um triângulo isósceles, obtemos que os ângulos e serão:
Passo 2
Em seguida, como queremos o valor de , tratemos de determinar o quanto vale o lado , já sabendo o valor de :
E também precisamos do valor de , né? Por isso, façamos:
Obtido o valor de , para encontrar , basta fazer o seguinte cálculo:
Pronto!! Encontrados e , para achar , usemos a relação da tangente do ângulo:
Passo 3
Como já sabemos o valor de , partiu fazer o triângulo de forças agora:
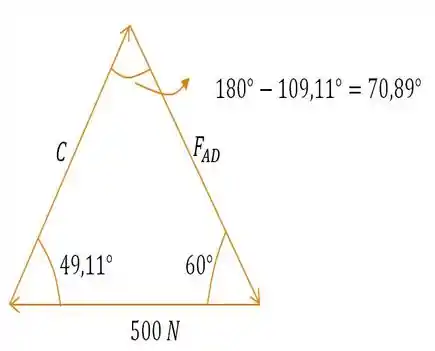
E em seguida, tratemos de usar a leis dos senos para descobrir quanto vale cada força:
Onde primeiramente, tratemos de descobrir o valor de :
E depois, façamos o cálculo para força :
E olha só que beleza! Encontramos as repsotas para as letras (a) e (b) do nosso problema.
Resposta
a)
b)