Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 79
79. Usando o método da seção , resolva o problema .
Passo 1
a) Bom! Primeiramente para o caso em que ; façamos o diagrama de corpo livre do nosso sistema:
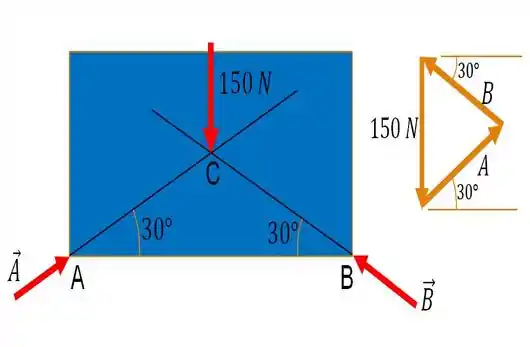
Como visto na figura acima, as reações em e irão se interceptar em um ponto comum que chamaremos de . Dispondo essas forças juntamente com a força de , vemos que elas formam um triângulo equilátero:
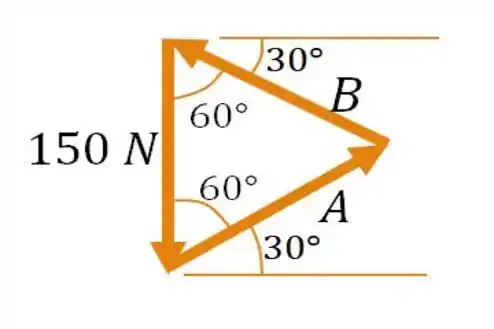
Baseado nisso, como no triângulo equilátero, os dois lados são iguais; tá na cara que as nossas forças serão:
Passo 2
b) Resolvida a primeira letra, vamos partir para essa segunda; onde a altura é de .
E então, vamos obter o ângulo :
Passo 3
E agora, vamos fazer o triângulo de forças com as três forças que temos na imagem do :
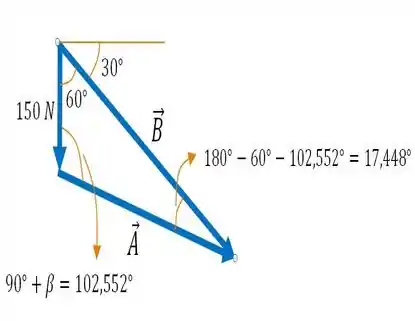
Em seguida, tratemos de usar a leis dos senos para descobrir quanto vale cada força:
Onde primeiramente, tratemos de descobrir o valor de :
E depois, façamos o cálculo para força :
Resposta
a)
b)