Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 78
78. Resolva o problema considerando que a força de aplicada em é horizontal e direcionada para a esquerda:
Passo 1
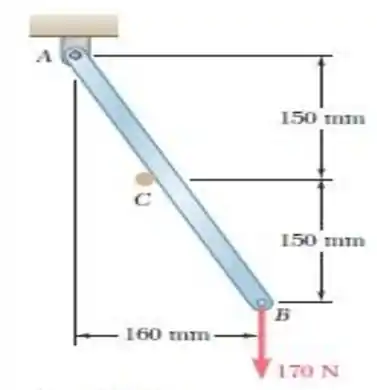
Bom! Primeiramente façamos o esboço do problema, considerando as forças que estarão presentes no nosso elemento . Ahhn! E as direções dessas forças; bom; irão estar sendo apontadas para o ponto :
Baseado nisso, a primeira coisa que temos que fazer é descobrir o quanto vale o ângulo presente na figura acima:
Agora vem ai a parte interessante! Lembra lá daqueles casos do ensino fundamental, em que com três relaçõezinhas básica, podíamos dizer se dois triângulos eram ou não congruentes. Repara nos triângulos e . Bom, eles tem o lado em comum. Os lados e são iguais, já que é o ponto médio de , e por fim, os ângulos e também são iguais, com um valor de ; onde é a mediatriz. Logo, os triângulos e são congruentes. Isso implica que o triângulo é isósceles, ou seja:
Passo 2
E agora, vamos fazer o triângulo de forças com as três forças que temos na imagem do :
Essa belezinha aí é um triângulo isósceles, o que implica que:
E em seguida, usemos a lei dos senos para descobrir o valor de :
Como :