Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 85b
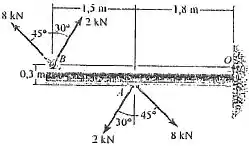
85. Determine o momento de binário resultante que age sobre a viga. Resolva o problema de duas maneiras;
(b) some os momentos em relação ao ponto .
Passo 1
Fala, querido! A gente quer o momento resultante na viga.
Ele pede para determinar em relação ao ponto . E como isso nos ajuda? Quer dizer que as forças que tem como ponto de aplicação o ponto não geram momento em relação a ele, então a gente pode ignorar elas. Então somente as forças em geram momento.
Vamos calcular o momento binário usando a análise escalar:
Onde é a intensidade das forças, e é perpendicular a . é a distância da linha de ação da força ao ponto onde queremos o momento, no caso, .
Teremos que decompor nossas forças em suas componentes horizontal e vertical, para resolver o problema, porque assim é mais fácil achar para cada caso.
O momento binário resultante é a soma dos momentos binários das forças.
Vamos adotar o sentido horário como positivo.
Passo 2
Vamos começar pelas componentes horizontais das forças em . Repara que a linha de ação de ambas está distante do ponto , então esse vai ser nosso para essas duas forças.
Aí para decompor no eixo horizontal, a gente a multiplica por . Ela gera momento no sentido anti-horário, por isso entra negativo na continha.
Já para a força de , multiplicamos seu valor por . E como ela gera momento no sentido horário, ele fica positivo.
Somando o momento causado por essas duas forças, temos:
Passo 3
Agora as componentes verticais das forças em . Repara que a linha de ação de ambas está distante do ponto , então esse vai ser nosso para essas duas forças.
Aí para decompor no eixo vertical, a gente a multiplica por . Ela gera momento no sentido horário, por isso entra positivo na continha.
Já para a força de , multiplicamos seu valor por . E como ela gera momento no sentido horário, ele fica positivo também.
Somando o momento causado por essas duas forças, temos:
Passo 4
Calculando o somatório de momentos em relação a .
Resposta
O momento de binário é: