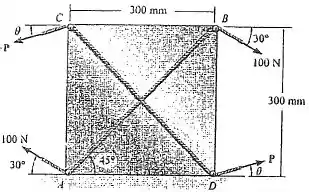
82. A corda passando por dois pinos e do quadro está sujeita a uma tração de . Determine a tração mínima e a orientação da corda passando pelos pinos e de modo que o momento de binário resultante produzido pelas duas cordas seja , horário.

A orientação de que produz a tração mínima é 45° já que os valores de seno e cosseno são os mesmos para esse ângulo, logo a tração tem a mesma contribuição na vertical e na horizontal.

Então o que o enunciado quer também é achar um que produza um momento binário que junto com o momento binário de seja igual a .

Vamos calcular o momento binário usando a análise escalar:

Onde é a intensidade das forças e é a distância perpendicular ou braço de momento entre as forças.

Teremos que decompor nossas forças, pois temos momentos referentes tanto as componentes horizontais, quanto verticais.

O momento binário resultante é a soma dos momentos binários das forças.

Vamos adotar o sentido horário como positivo.