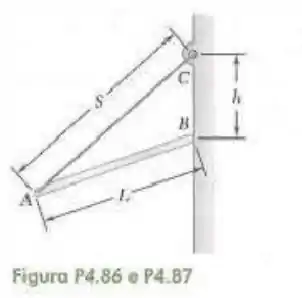
86- Uma haste delgada de comprimento é mantida em equilíbrio, tal como mostra a figura, com uma extremidade contra uma parede sem atrito e a outra presa a uma corda de comprimento . Deduza uma expressão para a distância em termos de e . Mostre que essa posição de equilíbrio não existe se .
Passo 1
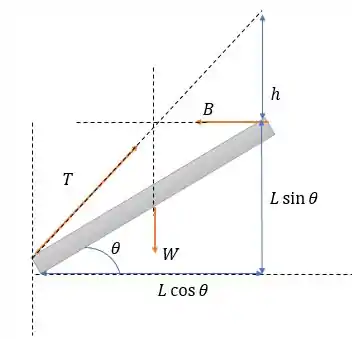
Considerando que essa haste tem um peso igual a e a força no cabo igual a , nós poderemos escrever o diagrama de forças nessa haste com as seguintes forças.
Passo 2
Se aplicarmos Pitágoras nesse triângulo retângulo nós teremos:
Porém é uma variável que não ‘’existe’’ no problema, nós que colocamos ele ai. Nós precisamos correlacionar ele somente com com ou com para podermos continuar de alguma forma.
E para isso vamos desenhar o diagrama de forças de outra maneira.

Pois para haver equilíbrio as forças devem se encontrar acima da posição do centro de gravidade, tendo na horizontal distâncias iguais a .
Então por semelhança de triângulos conseguimos ver que:
Logo se substituirmos isso nós teremos:
Passo 3
Agora existe uma propriedade da condição de existência de um triângulo que nos diz que se tivermos um triângulo de lados e esses lados obrigatoriamente terão que ter tamanhos iguais a:
Logo o lado do triângulo de lados iguais a e será:
Como então pode tirar o módulo:
Como então:
Elevando tudo ao quadrado:
Multiplicando todo mundo por :
Somando em todo mundo:
Agora diminuindo de todo mundo:
O que é algo como:
Na primeira parte da igualdade temos:
E na segunda:
Nenhuma delas aponta para e na verdade a segunda é impossível pois não pode ser negativo. Sendo descartado.