Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 73
72. Determine as reações em e quando .
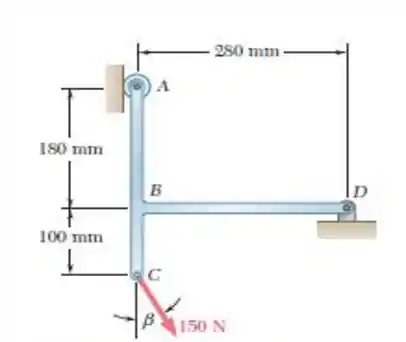
Passo 1
Bom! Primeiramente façamos o esboço do problema, considerando as forças que estarão presentes no elemento .
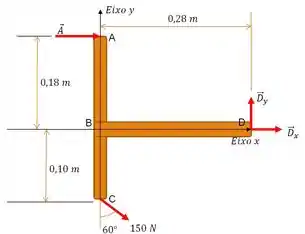
Passo 2
Baseado nisso, façamos o somatório das forças no ponto , para ver se podemos encontrar alguma força de nosso interesse:
Opa!! Até aí tudo bem! Já encontramos a força ! O que acha de aplicarmos o somatório das forças na direção ; já que só tem três forças agindo naquela direção e uma delas é a força :
E depois, façamos o somatório das forças na direção :
Passo 3
Agora que já encontramos e , temos que:
E como as componentes e formam um triângulo retângulo:
Finalmente, para achar o ângulo entre as forças e , basta saber que:
Pronto! Resposta encontrada!
Resposta
Exercícios de Livros Relacionados
Desenhe o diagrama de Corpo Livre da lança do guindaste AB, que possui peso 3,25 kN e um centro de gravidade em G. O apoio é sustentado por um pino em A em um cabo em BC. A carga de 6,25 kN é suspensa
Determine as componentes horizontais e verticais da reação no pino A e a tração desenvolvida no cabo BC usado para sustentar a estrutura de aço
Determine a tração na corda e as componentes horizontal e vertical da reação no apoio A da viga do problema 4
13. Determine as reações nos apoios da treliça no Problema 5.5 .
Compare a força exercida sobre a ponta do pé e sobre o calcanhar de uma mulher de 600 N quando ela está usando sapatos comuns e salto alto . Assuma que todo o seu peso está sobre um único pé e as reaç