Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 228
Ache o ângulo que colocará o centro de massa do anel fino a uma distância do centro do arco.
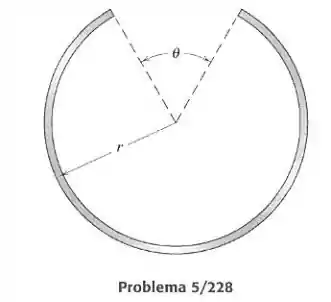
Passo 1
Pela simetria, sabemos que o centro de massa do anel estará no eixo que passa no centro e no meio da abertura de ângulo . Vamos então calcular a coordenada do centro de massa, sendo a origem o centro do anel e o eixo apontado para baixo. Dividindo o anel em elementos de tamanho infinitesimal , a fórmula da coordenada do CM será:
Passo 2
Observamos na figura um elemento do anel.
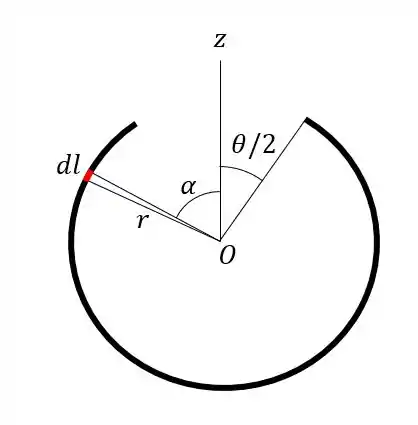
Cada elemento possui uma coordenada dada por:
E o ângulo varia de a . Então a nossa integral fica:
Passo 3
O comprimento do anel é:
Então finalmente temos a expressão para a coordenada do CM:
Passo 4
Queremos que esse valor seja igual a . Então:
Resolvendo a equação, obtemos o valor:
Resposta
Exercícios de Livros Relacionados
Localize o centroide z - do sólido.
Localiza o centroide z - do sólido homogêneo formado girando-se a área sombreada em torno do eixo y .
Localize o centroide y - do sólido homogêneo formado girando-se a área sombreada em torno do eixo y .
Localize o centroide z - do frustum sólido homogêneo do paraboloide formada girando-se a área sombreada em torno do eixo z .
Determine a massa e a localização do centro de massa y - do hemisfério formado girando-se a área sombreada em torno do eixo y . A densidade em qualquer ponto no hemisfério pode ser definida por ρ = ρ