Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 119
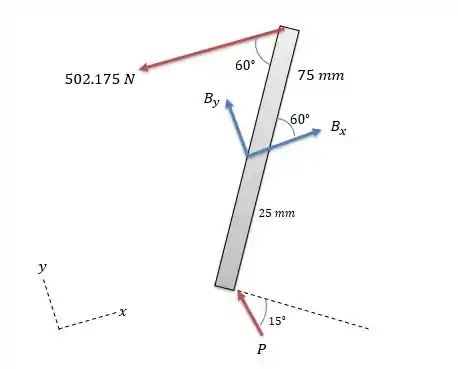
119- O mecanismo de poda de uma serra com cabo está mostrado no momento em que ele corta um galho, . Para a posição particular mostrada, a corda de fixação é paralela ao cabo e suporta uma força de tração de . Determine a força cisalhante aplicada ao galho pelo cortador e a força total suportada pelo pino em . A força exercida pela mola de retorno em é pequena e pode ser desprezada.
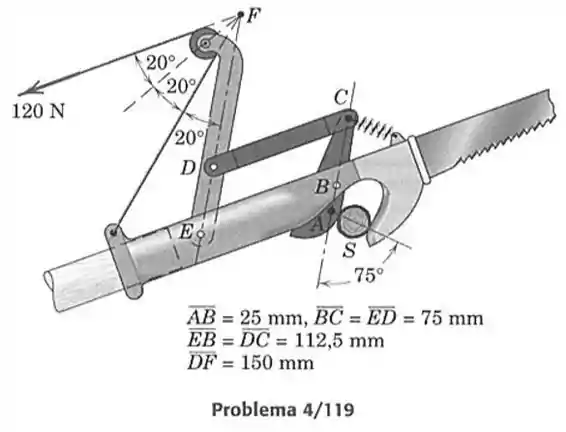
Passo 1
O cabo de tração que aguenta a força de é um multiplicador de força uma vez que a carcaça do mecanismo faz reação a força.
Primeiro vamos calcular a força resultante e a direção da mesma em relação a barra , para isso vamos fazer uso do triângulo isósceles na figura abaixo.
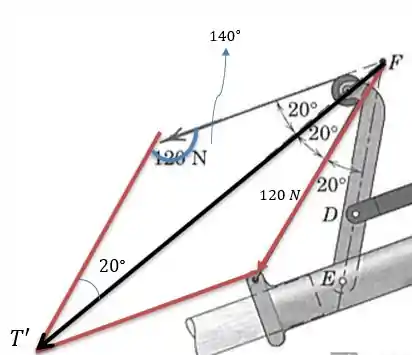
O valor de é dado pela lei dos cossenos:
Passo 2
Agora podemos calcular as forças de reação em e a força no elemento que servirá de apoio para calcular a força cisalhante no galho, para isso vamos desenhar o sistema de forças na barra .
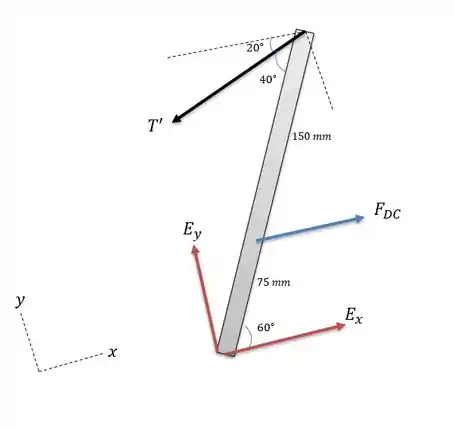
Fazendo a somatória dos momentos em nós encontraremos o valor da força . Fazendo a com que as forças fiquem perpendiculares a barra nós teremos a seguinte equação:
Agora vamos encontrar as reações em . Fazendo a somatória das forças verticais nós teremos:
Agora a somatória das forças horizontais:
Agora a força de reação no pino será o módulo igual a:
Passo 3
Agora vamos calcular a força que corta o galho. Para isso vamos fazer a somatória dos momentos em tal como no sistema de forças na barra abaixo.
