Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 110

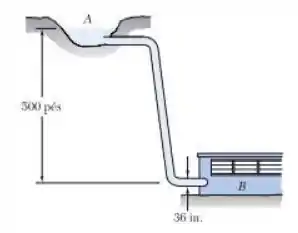
Uma adutora de aço tem diâmetro externo de 36   i n , uma espessura de parede 0,5   i n e conecta um reservatório em A com uma estação geradora de energia em B . Sabendo que a densidade da água é de 62,4   l b / p é s 3 determine a tensão normal máxima e a tensão de cisalhamento máxima na adutora sob condições estáticas.

Passo 1

Fala aí, galerinha. Tudo certo? Vamos para mais uma questão de mecânica pra tirar aquele notão na prova.

Este problema pede para determinarmos tensão normal máxima e a tensão de cisalhamento máxima na adutora sob condições estáticas. Primeiro, vamos determinar o raio da adutora, ele é dado por:

r = d 2 - t

Onde t é a espessura de parede. Logo, substituindo:

r = 36 2 - 0,5 r = 17,5   i n

Em seguida, temos que determinar a pressão no ponto A . Para isso, vamos utilizar a seguinte relação:

p = ρ h p = 62,4 500 p = 216,67   p s i

Agora que temos a pressão, o raio e a espessurada parede interna, podemos encontrar a tensão tangencial. Ela vai ser dada por:

σ 1 = p r t

Substituindo:

σ 1 = 216,67 17,5 0,5 σ 1 = 7583   p s i

Com isso, temos que a tensão normal máxima vai ser igual a tensão tangencial. Logo

σ m á x = σ 1 σ m á x = 7,58   k s i

Passo 2

Por fim, temos que encontrar tensão de cisalhamento máxima na adutora sob condições estáticas. Sabemos que ela é dada por:

τ m á x = 1 2 ( σ m á x - σ m í n )

Opa, a gente já tem a tensão máxima, falta encontrar a tensão mínima. Sabemos que ela vai ser o inverso da pressão. Logo:

σ m í n = - p σ m í n = 217   p s i

Com isso, só falta substituirmos na relação da tensão de cisalhamento. Fica assim:

τ m á x = 1 2 7,58 - 217 τ m á x = 3,90   k s i

Isso é tudo, gurizada! Bora zerar esse livro?

Resposta

σ m á x = 7,58   k s i

τ m á x = 3,90   k s i

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tubo de 2m de comprimento é feito de um material elástico perfeitamente plástico como mostra a figura. Determine o torque aplicado T que submete o material da borda externa do tubo à deformação por
O tubo tem comprimento de 2m e é feito de um matrial elástico-plástico como mostra a figura. Determine o torque necessário só para tornar o material totalmente plástico. Qual é o ângulo de torção perm
O tubo de 2m de comprimento é feito de um material elástico-plástico como mostra a figura. Determine o torque aplicado T que submete o material da borda externa do tubo a uma deformação por cisalhamen
O eixo é feito de um material endurecido por deformação cujo diagrama τ - γ é mostrado na figura. Determine o torque T que deve ser aplicado ao eixo de modo a criar um núcleo elástico no eixo com raio
O tubo circular de aço A - 36 é submetido a um torque de 10 k N ⋅ m . Determine a tensão de cisalhamento no raio médio ρ = 60 m m e calcule o ângulo de torção do tubo se ele tiver 4 m de comprimento e