Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 142

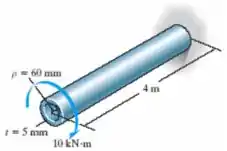
O tubo circular de aço A - 36 é submetido a um torque de 10 k N ⋅ m . Determine a tensão de cisalhamento no raio médio ρ = 60 m m e calcule o ângulo de torção do tubo se ele tiver 4 m de comprimento e estiver preso em sua extremidade mais distante. Resolva o problema usando as equações 5.7 ,   5.15 ,   5.18 ,   5.20 .

Passo 1

A questão nos dá os dados: G = 75   G P a (tabelado para o aço em mencionado) ,     T = 10 k N ⋅ m ,     ρ = 60 m m ,   L = 4 m ,   t = 5 m m , e nos pede o valor do ângulo de torção ϕ e tensão de cisalhamento em ρ = 60   m m . (o raio médio)

Temos que ter atenção a questão, pois ela tem várias respostas dependendo de quais equações utilizamos.

Equação 5.7: τ = T c J

Equação 5.15: ϕ = T L J G

Equação 5.18: τ = T 2 t A m

Equação 5.20: ϕ = T L 4 A m 2 G ∮ d s t

Percebe que as duas primeiras equações são referentes a torsão em uma seção circular e as duas últimas em tubos de paredes finas.

Por isso, a gente só vai aplicar a equação 5.15 no resultado da 5.7 e só vai aplicar a 5.20 no resultado da 5.18 , ok?

Basicamente vamos calcular a mesma coisa por caminhos diferentes. Bora!

Passo 2

Por conveniência, vamos primeiro calcular as propriedades geométricas que serão úteis em todas as equações.

Ele nos deu o raio médio, que é a média entre o raio interno e o raio externo. Vamos achar esses carinhas a partir disso então:

Raio externo:

R = ρ + t 2 = 60 + 5 2 = 62,5   m m

Raio interno:

r = ρ - t 2 = 60 - 5 2 = 57,5   m m

Cálculo do momento polar de inércia:

J = π 2 R 4 - r 4 = π 2 62,5 4 - 57,5 4 ⇒ J = 6,797 ⋅ 10 6   m m 4

Área interna média:

A M = π ρ 2 = π ⋅ 60 2 ⇒ A M = 11309,73   m m 2

Passo 3

Aplicando a Equação 5.7, para achar a tensão, o ponto de aplicação é o raio médio ρ

τ = T c J

τ = T ⋅ ρ J

Substituindo nossos dados:

τ = 10 ⋅ 60 6,8 ⋅ 10 6 ⋅ k N ⋅ m ⋅ m m m m 4

τ = 10 ⋅ 60 6,8 ⋅ 10 6 ⋅ 10 3 N ⋅ 10 3   m m ⋅ m m m m 4

τ = 88,23   M P a

Passo 4

Aplicando a Equação 5.15 para achar o ângulo

ϕ = T L J G

ϕ = 10 ⋅ 4 6,8 ⋅ 10 6 ⋅ 75 ⋅ 10 9 ⋅ k N ⋅ m ⋅ m m m 4 ⋅ P a

ϕ = 10 ⋅ 4 6,8 ⋅ 10 6 ⋅ 75 ⋅ 10 9 ⋅ ( 10 3 N ) ⋅ m ⋅ m ( 10 - 12 ⋅ m 4 ) ⋅ P a

ϕ = 10 ⋅ 4 6,8 ⋅ 75 ⋅ 10 3 10 6 ⋅ 10 9 ⋅ 10 - 12 ⋅ N ⋅ m ⋅ m m 4 ⋅ P a

ϕ = 0,07846   r a d

ϕ = 4,495 º

Passo 5

Aplicando a Equação 5.18, de tubo de paredes finas, para achar a tensão:

τ = T 2 t A m

τ = 10 2 ⋅ 5 ⋅ 11309,73 ⋅ k N ⋅ m m m ⋅ m m 2

τ = 10 2 ⋅ 5 ⋅ 11309,73 ⋅ 10 3 ⋅ N ⋅ 10 3 ⋅ m m m m ⋅ m m 2

τ = 88,42   M P a

Essa expressão já dá a tensão no raio médio, beleza?

Passo 6

Aplicando a Equação 5.20:

ϕ = T L 4 A m 2 G ∮ d s t

Vale notar que t   (a expessura) é constante

ϕ = T L 4 A m 2 G ⋅ t ∮ d s

Agora um bizu: Observe que a nossa seção transversal é uma circunferência, o que implica dizer que esta integral de linha com integrando 1 na verdade é o perímetro da circunferência, em ρ = 60   m m .

ϕ = T L 4 A m 2 G ⋅ t ⋅ 2 π ρ

ϕ = 10 ⋅ 4 4 ⋅ 11309,73 2 ⋅ 75 ⋅ 5 ⋅ 2 π ⋅ 60 ⋅ k N ⋅ m m m 4 ⋅ G P a ⋅ m m ⋅ m m

Fazendo as simplificações:

ϕ = 10 ⋅ 4 4 ⋅ 11309,73 2 ⋅ 75 ⋅ 5 ⋅ 2 π ⋅ 60 ⋅ 10 3 N ⋅ m ⋅ 10 - 3 m 10 - 12 m 4 ⋅ 10 9 P a ⋅ 10 - 3 m

ϕ = 0,0786   r a d

ϕ = 4,503 º

Resposta

Equação 5.7: τ = 88,23   M P a  

Equação 5.15: ϕ = 4,495 º  

Equação 5.18: τ = 88.42   M P a

Equação 5.20: ϕ = 4,503 º

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a tensão normal em uma bola de basquete de 300 mm de diâmetro externo e espessura de parede de 3,0 mm que é inflada a uma pressão manométrica de 120 kPa.
O tanque de armazenagem cilíndrico não pressurizado indicado na figura tem uma parede com espessura de 5 mm e é feito de aço com um limite de resistência de 400 MPa na tração. Determine a altura máxim
Um vaso de pressão esférico, com diâmetro externo de 750 mm, deve ser fabricado com um aço que tem um limite de tensão σ L = 400M P a . Sabendo que se deseja um coeficiente de segurança de 4 e que a p
Para o tanque de armazenagem do Problema 7.104, determine a tensão normal máxima e a tensão de cisalhamento máxima na parede cilíndrica quando o tanque estiver totalmente cheio (h = 14,5 m).
Um tubo de aço padrão pesado com 12 in. de diâmetro nominal suporta água sob pressão de 400 psi. (a) Sabendo que o diâmetro externo é de 12,75 in. e que a espessura da parede é de 0,375 in., determine