Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 125

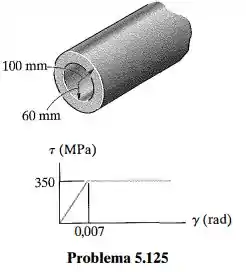
O tubo tem comprimento de 2   m e é feito de um matrial elástico-plástico como mostra a figura. Determine o torque necessário só para tornar o material totalmente plástico. Qual é o ângulo de torção permanente do tubo quando esse torque é removido?

Passo 1

Dados da questão: L = 2 m ,   r i = 60 m m ,   r O = 100 m m ,   τ e = 350 M P a ,   τ e = 0,007 , Material elástico-plástico.

A afimarção “só para tornar o material totalmente plástico” nos garate que:

  • Não há núcleo elástico
  • A deformação sofrida no raio interno é a menor possível para atingir o regime plástico, ou seja, a deformação de escoamento: γ = γ e = 0,007   r a d

A questão pede:

  • O torque plástico     T p = ?
  • Ângulo de torção residual   ϕ r = ?

A nossa estratégia de resolução será: Primeiro usaremos a Equação 5.23 para determinar o torque plástico. Depois utilizamos a deformação plástica no raio interno para definir o ângulo de torção plástico. Depois podemos utilizar o valor do torque plástico para determinar a recuperação elástica. E finalizamos encontrado o valor da deformação residual.

Passo 2

Inicialmente vamos calcular alguns valores que serão úteis.

O momento de inércia:

J = π 2 ( r O 3 - r i 3 )

J = π 2 ( 100 3 - 0,060 3 )

J = 43,52 π ⋅ 10 - 6   m - 4

E o coeficiente de cisalhamento pode ser encontrado pelo gráfico

G = τ e γ e

G = 450   M P a 0,007   r a d

G = 50   G P a

Passo 3

Agora aplicamos a equação 5.23 com os limites de integração do raio interno ao raio externo

τ P = 2 π ⋅ ∫ r i r O τ ⋅ ρ 2 d ρ

Como não há núcleo elástico, a tensão é constante e igual à tensão de escoamento: τ = τ e

τ P = 2 π ⋅ ∫ r i r O τ e ⋅ ρ 2 d ρ

τ P = 2 π ⋅ τ e ⋅ 1 3 ( r O 3 - r i 3 )

Substituíndo os valores:   r i = 0,060 m ,   r O = 0,100   m e τ e = 350   M P a ,

τ P = 2 π ⋅ ( 350 ⋅ 10 6 ) ⋅ 1 3 ( 0,1 3 - 0,06 3 )

τ P = 574,7   k N ⋅ m

Passo 4

Como é defindo que a deformação plástica no eixo interno é igual a deformação de escoamento, então podemos calcular o ângulo de torção plástico:

ϕ p = γ P ⋅ L r i

Aplicando os valores: r i = 0,060 m ,   L = 2 m e γ P = 0,007   r a d

ϕ P = 0,007 ⋅ 2   0,060

ϕ P = 0,233   r a d

Passo 5

Na recuperação elástica, uma torção de intensidade T P atua em sentido inverso “destorcendo” o material de maneira elástica. O que nos permite aplicar a Equação 5.15

ϕ ' = T P L G J

Aplicando os valores: J = 43,52 π ⋅ 10 - 6   m - 4 ,   τ P = 574,7 ⋅ 10 3   N ⋅ m ,   L = 2 m e G = 50 ⋅ 10 9   P a

ϕ ' = 574,7 ⋅ 10 3 ⋅ 2 50 ⋅ 10 9 ⋅ 43,52 π ⋅ 10 - 6

ϕ ' = 0,168

Passo 6

A deformação residual é:

ϕ r = ϕ P - ϕ '

Substituíndo os valores: ϕ P = 0,233   r a d e ϕ ' = 0,168   r a d

ϕ r = 0,233 - 0,168

ϕ r = 0,065   r a d

ϕ r = 3,72 º

Resposta

ϕ r = 3,72 º

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um vaso de pressão com diâmetro interno de 254m m , espessura de 6,35 m m e comprimento de 1219m m é soldado em espiral e possui duas tampas laterais rígidas. A pressão manométrica dentro do vaso é de
Para o tanque do problema 7,117 , determine a maior pressão manométrica admissível, sabendo que a tensão normal perpendicular à solda é 18k s i e a tensão de cisalhamento admissível paralela à solda é
Para o problema 7.117 , determine o intervalo de valores de β que podem ser utilizados considerando que a tensão de cisalhamento paralela à solda não deve ultrapassar 1350 psi quando a pressão manomét
Um torque de intensidade T = 12k Nm é aplicado à extremidade de um tanque que contém ar comprimido sob uma pressão de 8M P a . Sabendo que o tanque tem um diâmetro interno de 180m m e uma espessura de
O tanque de pressão mostrado na figura tem uma parede com espessura de 0,375i n e possui emendas de solda de topo formando um ângulo β = 20 ° com um plano transversal. Para uma pressão manométrica de