Uma aeronave decola em e se eleva em um ângulo constante com inclinação de para no plano vertical - com uma velocidade constante . A aeronave é rastreada por radar em . Para a posição , determine os valores de , e .
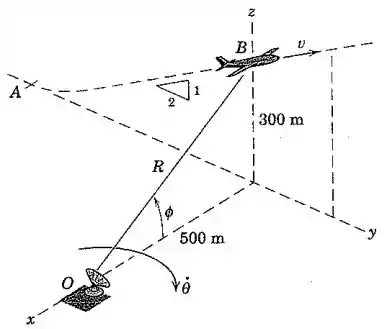
Passo 1
O ângulo que a trajetória do avião faz com a horizontal satisfaz:
Então, a velocidade pode ser decomposta assim:
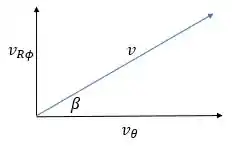
Passo 2
A velocidade pode ser decomposta novamente, assim:
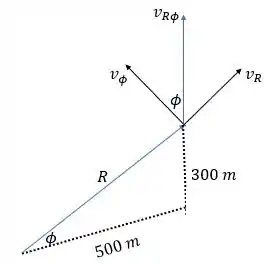
Para calcular cada componente, achamos o ângulo :
Então:
Mais tarde também precisaremos da distância , então calculamos por Teorema de Pitágoras:
Passo 3
Agora, vamos lembrar como se escreve a velocidade nessas coordenadas esféricas:
Então, podemos igualar cada componente dessa expressão com sua respectiva componente já calculada, assim ó:
Com a primeira equação, obtemos:
Com a segunda:
Com a última: