Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 21

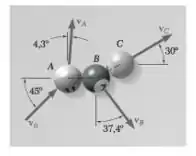
Em um jogo de bilhar, a bola A se move com uma velocidade v0 quando ela atinge as bolas B e C, que estão em repouso e alinhadas conforme mostrado na figura. Sabendo que após a colisão as três bolas se movem nas direções indicadas e que v0 = 4 m/s e v0 = 2 m/s, determine a intensidade da velocidade da bola A e da bola B.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Como foi de fim de ano?? Preparado para voltar?? Então vamos lá Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos a figura e dizermos qual o tempo e a velocidade. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, vamos lembrar que não existem forças externas horizontais que atuam durante os impactos, portanto o centro de massa G do sistema se move em velocidade constante, além de ser dado pelo vetor posição r.

Segundo a conservação de energia nas direções x e y, teremos, respectivamente:

m 4 cos ⁡ 45 = m v Z sin ⁡ 4,3 + m v B sin ⁡ 37,4 + m 2 cos ⁡ 30

0,07498 v A - 0,60738   v B = 1,096

m 4 s in ⁡ 45 = m v Z cos ⁡ 4,3 + m v B cos ⁡ 37,4 + m 2 s in ⁡ 30

0,99719   v A - 0,7944 v B = 1,828

Eaii?? Chegou bem até aqui?? Então bora substituir os valores e continuar nossa conta.

0,66524   v A = 1,98096

0,66524   v B = 0,95586

Passo 3

Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!

v A = 2,9778   m / s

v B = 1,4369   m / s

Resposta

v A = 2,9778   m / s

v B = 1,4369   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A profundidade da água que escoa do um canal de seção transversal retangular de largura b a uma velocidade v1 e a uma profundidade d 1 aumenta para uma profundidade d 2 em um ressalto hidráulico. Expr
Em uma roda de turbina Pelton, o jato de água é defletido por uma série de pás de modo que a taxa com a qual a água é defletida pelas pás é igual à taxa com a qual a água sai do bocal ( Δ m / Δ t = A
14.49. Três esferas idênticas A, B e C, que podem deslizar livremente sobre uma superfície horizontal sem atrito, estão ligadas por meios de cordas inelásticas e inextensíveis a um pequeno anel D loca
14.47. Duas pequenas esferas A e B, de massas 2,5 kg e 1 kg, respectivamente, estão unidas por uma barra rígida de massa desprezível. As duas esferas estão em repouso sobre uma superfície horizontal s
14.50. Resolver o Problema 14.49, considerando que 45°.