Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 210
A aeronave com equipamento de detecção por radar está voando horizontalmente a uma altitude de e está aumentando sua velocidade na taxa de cada segundo. Seu radar capta uma aeronave voando na mesma direção e no mesmo plano vertical a uma altitude de . Se tem uma velocidade de no instante em que , determine os valores de e neste mesmo instante se tem uma velocidade constante de .
Passo 1
Primeiramente, vamos calcular a velocidade relativa de em relação a (que só existe na direção do eixo ) no instante em que :
Note que os valores de e são valores de em relação a . Então, usando essas coordenadas polares, podemos escrever a velocidade relativa também assim:
Porém, já achamos o módulo dessa velocidade, então também podemos escrever assim:
Então, igualando os componentes em , obtemos:
E em :
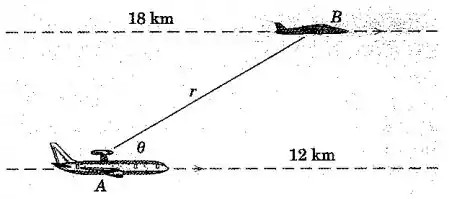
Olhando pra figura, a distância vertical é de , então:
Substituímos isso de volta na equação:
Passo 2
De modo bastante parecido, vamos calcular a aceleração relativa de em relação a , que só existe na direção do eixo :
Mas a fórmula geral da aceleração em coordenadas polares nos dará:
Como já achamos o módulo dessa aceleração, podemos também escrever assim:
Então, igualando os componentes em , obtemos:
Lembre-se que já calculamos , e , então podemos substituir esses valores:
Agora igualando em :