Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 209

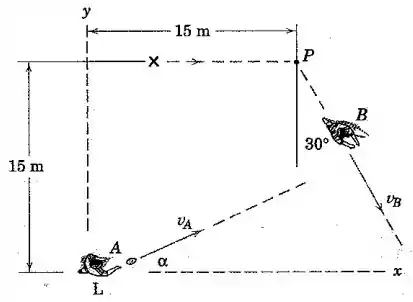
Após partir da posição marcada com um “ x ”, um jogador de futebol americano B corre modificando a trajetória no padrão apresentado, fazendo um corte em P e depois correndo com uma velocidade constante v B = 7   m / s na direção mostrada. O lançador arremessa a bola com uma velocidade horizontal de 30   m / s no instante em que o jogador passa pelo ponto P . Determine o ângulo α no qual o lançador deve jogar a bola, e a velocidade da bola em relação ao jogador quando a bola é agarrada. Despreze qualquer movimento vertical da bola.

Passo 1

Pessoal, pra tentar achar o ângulo α , a gente pode escrever as equações do movimento da bola A e do jogador B em cada direção e verificar em que hipótese eles se cruzam:

x A = v A cos ⁡ α t = 30 cos ⁡ α t

y A = v A   s e n   α   t = 30   s e n   α   t

x B = 15 + 7   s e n   30 °   t = 15 + 3,5   t

y B = 15 - 7 cos ⁡ 30 ° t = 15 - 6,06   t

Igualando x A = x B e y A = y B , obtemos um sistema de duas equações e duas incógnitas:

30 cos ⁡ α t = 15 + 3,5   t

30   s e n   α   t = 15 - 6,06   t

Passo 2

Agora vamos resolver o sistema. Isolamos t na primeira equação:

t = 15 30 cos ⁡ α - 3,5

E aí substituímos na segunda:

30   s e n   α 15 30 cos ⁡ α - 3,5 = 15 - 6,06 15 30 cos ⁡ α - 3,5

Multiplicamos toda a equação por 30 cos ⁡ α - 3,5 :

450   s e n   α = 450 cos ⁡ α - 52,5 - 90,9

450 1 - cos 2 ⁡ α = 450 cos ⁡ α - 143,4

450 1 - cos 2 ⁡ α 2 = 450 cos ⁡ α - 143,4 2

202500 1 - cos 2 ⁡ α = 202500 cos 2 ⁡ α - 129060 cos ⁡ α + 20564

405000 cos 2 ⁡ α - 129060 cos ⁡ α - 181936 = 0

Resolvendo essa equação do segundo grau, obtemos:

cos ⁡ α = - 0,5296                     o u                   cos ⁡ α = 0,8483

Para obter um ângulo α positivo, só consideramos a solução positiva:

cos ⁡ α = 0,8483

α = cos - 1 ⁡ 0,8483

α = 32 °

Passo 3

Vetorialmente, as velocidades v A e v B da bola A e do jogador B podem ser escritas assim:

v A = v A cos ⁡ α i + v A   s e n   α   j = 30 cos ⁡ 32 ° i + 30   s e n   32 °   j

v A = 25,44   i + 15,9   j

v B = 7   s e n   30 °   i - 7 cos ⁡ 30 ° j

v B = 3,5   i - 6,06   j

A velocidade relativa v A B da bola A em relação ao jogador B pode ser dada por:

v A B = v A - v B

v A B = 25,44   i + 15,9   j - 3,5   i - 6,06   j

v A B = 21,9   i + 21,9   j   m / s

Resposta

α = 32 °

v A B = 21,9   i + 21,9   j   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um satélite da Terra é colocado em uma órbita circular polar a uma altitude de 240k m , que requer uma velocidade orbital de 27940k m / h em relação ao centro da Terra considerada fixa no espaço. No c
Para as condições do Prob. 2/203, determine os valores de r ¨ e θ ¨ conforme medidos por um observador no carro B no instante representado. Use os resultados para r ˙ e θ ˙ citados nas respostas para
O avião A está voando horizontalmente com uma velocidade constante de 200k m / h e está rebocando o planador B , que está ganhando altitude. Se o cabo de reboque tem um comprimento r = 60m e θ está au
Os satélites A e B estão em uma órbita circular de altitude h = 1500k m . Determine o módulo da aceleração do satélite B em relação a um observador sem rotação no satélite A . Utilize g 0 = 9,825m / s
A nave espacial S aproxima-se do planeta Marte ao longo de uma trajetória b - b no plano orbital de Marte com uma velocidade absoluta de 19k m / s . Marte tem uma velocidade de 24,1k m / s ao longo de