Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 205
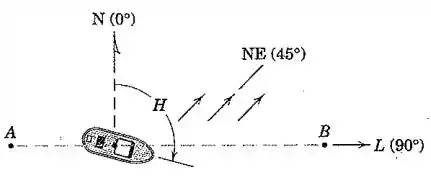
O capitão de um pequeno navio capaz de atingir uma velocidade de nós através de águas calmas deseja definir um curso que levará o barco diretamente para leste a partir de até por uma distância de milhas marítimas. Para levar em consideração uma corrente constante de nós fluindo para nordeste, determine sua leitura necessária na bússola, medida no sentido horário a partir do norte até o grau mais próximo. Também determine o tempo da viagem. (Lembre-se de que nó é milha marítima por hora.)
Passo 1
Pessoal, vamos considerar como a velocidade da corrente, cujo módulo é nós, dirigida para nordeste:
e como a velocidade real do navio (em relação à Terra), dirigida para leste:
Além disso, será a velocidade relativa do navio em relação à água, com módulo igual a nós, e cuja direção é a que queremos conhecer:
Passo 2
Temos a seguinte relação entre as velocidades:
Se compararmos cada componente, obteremos duas equações:
Resolvendo a segunda equação:
Esse ângulo é dado em relação à horizontal. O ângulo em relação à vertical, , será:
Passo 3
Para calcular o tempo da viagem, precisamos saber o módulo da velocidade do navio. Podemos calcular isso por meio daquela primeira equação encontrada no passo anterior:
Como a distância viajada é , temos:
Ou seja, teremos .