Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 64

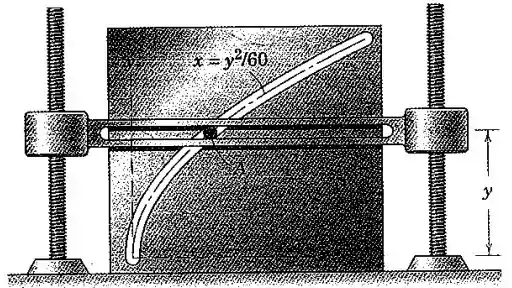
Para um determinado intervalo de movimento o pino A é forçado a se deslocar na ranhura fixa parabólica pelo braço horizontal com encaixe que é elevado na direção y a uma taxa constante de 30   m m / s . Todas as medidas são em milímetros e segundos. Calcule a velocidade v e aceleração a do pino A quando x = 60   m m .

Passo 1

Galera, temos que o pino A vai seguir a trajetória de uma parábola cuja equação é dada por:

x = y 2 60

Se derivarmos ambos os lados da equação em relação ao tempo, vamos obter uma relação interessante entre as velocidades vertical e horizontal do pino:

x ' = y 30 y '

v x = y 30 v y

Derivando mais uma vez, temos a relação entre as acelerações vertical e horizontal:

v x ' = y ' 30 v y + y 30 v y '

a x = v y 2 30 + y 30 a y

Passo 2

O enunciado nos diz que o braço é elevado verticalmente a uma taxa constante de 30   m m / s . Logo, podemos considerar que v y = 30   m m / s e a y = 0   m m / s 2 .

Bora substituir isso nas relações encontradas?

v x = y 30 v y = y 30 30 = y

a x = v y 2 30 + y 30 a y = 30 2 30 + y 30 0 = 30

Usando a relação da trajetória, temos, quando x = 60   m m :

v x = y = 60 x = 60   .   60 = 60   m m / s

a x = 30   m m / s 2

Passo 3

Beleza! Agora é só usar as seguintes fórmulas para encontrar o módulo da velocidade v e da aceleração a :

v = v x 2 + v y 2 = 60 2 + 30 2 ≈ 67   m m / s

a = a x 2 + a y 2 = 30 2 + 0 2 = 30   m m / s 2

Resposta

v = 67   m m / s

a = 30   m m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O centro de massa G de um atleta de salto em altura segue a trajetória mostrada. Determine a componente v 0 , medida no plano vertical da figura, da sua velocidade de impulsão e o ângulo θ se o ápice
Os movimentos x e y das guias A e B com ranhuras em ângulo reto controlam o movimento curvilíneo do pino P de conexão, que desliza nas duas ranhuras. Por um curto intervalo de tempo, os movimentos são
As coordenadas retangulares de uma partícula que se desloca no plano x - y são dadas por x = 3 cos ⁡ ( 4 t ) e y = 2s e n ( 4 t ) , onde o tempo t é expresso em segundos e x e y são expressos em metro
Se o tenista mostrado na figura dá o saque com uma velocidade v de 130k m / h em um ângulo θ = 5 ° , calcule a folga vertical h do centro da bola acima da rede e a distância s a partir da rede onde a
Elétrons são emitidos em A com uma velocidade u no ângulo θ para o espaço entre duas placas carregadas. O campo elétrico entre as placas é na direção E e repele os elétrons que se aproximam da placa s