Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 212
Em um dado instante após saltar do avião , um paraquedista está na posição mostrada e atingiu uma velocidade terminal (constante) . O avião possui a mesma velocidade constante , e após um período de voo horizontal começa a seguir a trajetória circular apresentada de raio .
(a) Determine a velocidade e a aceleração do avião em relação ao paraquedista.
(b) Determine a taxa de variação no tempo da velocidade do avião e o raio de curvatura da sua trajetória, as duas conforme observadas pelo paraquedista sem rotação.
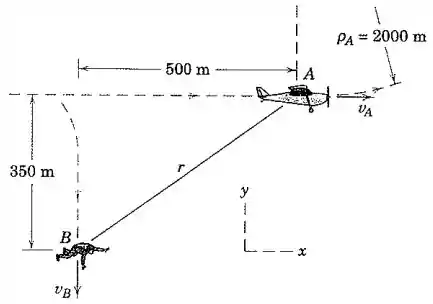
Passo 1
(a) A velocidade do avião é para a direita, e a velocidade do paraquedista é para baixo, então podemos escrever assim:
Portanto, a velocidade relativa do avião em relação ao paraquedista será:
Como ambos tem módulo de velocidade constante, a única aceleração presente será a aceleração normal (para cima) devido ao movimento circular do avião :
Passo 2
(b) Primeiro vamos achar que ângulo a velocidade relativa faz com a horizontal:
Então, pra determinar a taxa de variação no tempo da velocidade do avião vista pelo paraquedista, tudo que precisamos fazer é calcular a componente da aceleração relativa nessa direção, assim:
Passo 3
O valor que acabamos de calcular pode ser descrito como a aceleração tangencial do avião vista pelo paraquedista, ou seja, a taxa em que a velocidade dele aumenta em módulo, aos olhos do paraquedista.
Da mesma forma, temos a aceleração normal vista pelo paraquedista, que é a outra componente da aceleração relativa:
Assim, usando a fórmula de aceleração normal, podemos calcular o raio de curvatura visto pelo paraquedista desse modo:
Lembrando que , seu módulo é obtido:
Resposta
(a)
(b)