Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 15
As três pequenas esferas estão soldadas à estrutura leve rígida que está girando em um plano horizontal em torno de um eixo vertical através de com uma velocidade angular . Se um torque é aplicado à estrutura por segundos, calcule a nova velocidade angular .
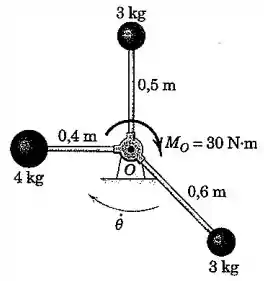
Passo 1
Vamos lembrar da seguinte equação:
No nosso caso, o momento resultante é a constante . Então:
Rearranjando os termos, obtemos a seguinte equação diferencial:
Agora, integraremos a equação obtida nos dois lados:
Passo 2
Nesse caso, teremos:
Então:
Substituímos os valores:
Resposta
Exercícios de Livros Relacionados
O anel esguio de 15 kg atinge o degrau de 20 mm de altura. Determine a menor velocidade angular ω 1 que o anel pode ter, de maneira que ele vá simplesmente rolar sobre o degrau em A sem deslizar.
A plataforma de 150 kg pode ser considerada como um disco circular. Dois homens, A e B, de 60 kg e 75 kg de massa, respectivamente, estão parados de pé na plataforma quando ela está em repouso. Se ele
Uma plataforma circular horizontal tem uma massa de 150 kg e um raio de giração k z = 2,4m em relação ao eizo z passando pelo seu centro O. A plataforma é livre para girar em torno do eixo z e está in
O corpo do satélite C tem uma massa de 200 kg e um raio de giração em relação ao eixo z de k z = 0,2m . Se o satélite gira em torno do eixo z com uma velocidade angular de 5 rev/s, quando os painéis s
Um homem de 75 kg salta para fora da plataorma circular com uma velocidade v m / p = 1,5m / s em relação à plataforma. Determine a velocidade angular da plataforma depois disso. Inicialmente o homem e