Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas fundamentais - Ex. 4
O carro de está sendo rebocado por um guincho. Se o guincho exerce uma força sobre o cabo, onde s é o deslocamento do carro em metros. Determine a velocidade escalar do carro quando , partindo do repouso. Despreze a resistência ao rolamento do carro.
Passo 1
Para obtermos a velocidade escalar do veículo, devemos primeiramente obter a equação do movimento. Do diagrama de corpo livre, temos:
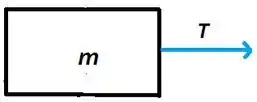
Sabendo que a tração desenvolvida no cabo é função do deslocamento, e igual, substituindo o valor da tração e massa na equação acima, teremos:
Passo 2
Podemos verificar que a aceleração do carro é função do deslocamento , ou seja, na medida em que o veículo se movimenta, a aceleração irá variar, então, não podemos utilizar as equações da cinemática para aceleração contante.
Para a resolução do problema, devemos desenvolver uma equação que relacione velocidade, aceleração e deslocamento. Sabemos que a velocidade e aceleração de um corpo é igual a taxa de variação do deslocamento e da velocidade em um determinado tempo, ou seja:
;
Isolando nas equações acima, temos:
Passo 3
Agora que encontramos uma equação que relaciona as variáveis , temos que substituir o valor da aceleração na equação acima, e integrar os dos lados da igualdade:
No enunciado do problema, o carro parte do repouso () em e, em m, teremos a velocidade instantânea, assim, devemos integrar em um intervalo de , e em um intervalo de :
Resposta
Em , o veículo terá uma velocidade de .