Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 13.Problemas - Ex. 4

A caminhonete de 2 Mg está se movendo A 15 m∕s quando os freios em todas suas rodas são aplicados, fazendo com que ele escorregue por uma distância de 10 m antes de chegar ao repolso. Determine a força horizontal desenvolvida no engaste C, e a força de atrito desenvolvida entre os pneus da caminhonete e a estrada durante este tempo. A massa total da lancha e do reboque é 1 Mg.

Passo 1

O primeiro passo para a solução do problema é obtermos a aceleração da caminhonete. Sabendo que o movimento ocorre com uma aceleração constante, podemos utilizar a equação de Torriceli para encontrarmos a aceleração da caminhonete:

v 2 = v 0 2   + 2 a ∆ s                       ( e q   d e   t o r r i c e l i )

Inicialmente, o veículo possui uma velocidade v 0 = 15 m∕s e, após os freios das rodas serem acionados, o veículo entrará em repolso ( v = 0 ) quando percorrer 10 m, portanto, a aceleração da caminhonete pode ser calculada da seguinte forma:

  a = v 2 - v 0 2 2 ∆ s = 0 2 - 15 2 2 × 10

a =   - 11,25   m / s 2

Passo 2

O próximo passo é encontrar a força desenvolvido no engaste C e a força de atrito

desenvolvida entre os pneus da caminhonete e a estrada. Inicialmente, precisamos obter a equação do movimento do reboque e da caminhonete. Sabendo que a aceleração da caminhonete é igual a do reboque, temos:

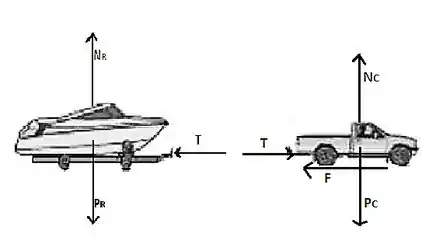
Diagrama de corpo livre do reboque:

∑ F x =   m r a

- T =   m r a

T = - m r a

T =   - 1000 × - 11,25 = 11,25 kN

Diagrama de corpo livre da caminhonete:

∑ F x =   m c a

T - F =   m c a

  F =   T - m c a

F =   11250 - 2000 × - 11,25 = 33,75   kN

Resposta

As forças desenvolvidas no engaste e nos pneus serão, respectivamente, 11,25 kN e 33,75   kN

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o peso absoluto e o peso em relação à Terra girando de um homem de 90k g , se ele está de pé sobre a superfície da Terra a uma latitude de 40 ° .
Calcule a distância d a partir do centro do Sol na qual uma partícula experimenta atrações iguais da Terra e do Sol. A partícula está restrita à linha que une os centros da Terra e do Sol. Justifique
O coeficiente de arrasto C A de um automóvel é determinado a partir da expressão C A = A 1 2 ρ v 2 S Onde A é a força de arrasto determinada experimentalmente em um túnel de vento, ρ é a massa específ
Para os vetores V → 1 e V → 2 dados, determine V 1 + V 2 , V → 1 + V → 2 , V 1 → - V → 2 , V 1 → × V 2 → , V 2 → × V 1 → e V 1 → ∙ V 2 → . Considere que os vetores sejam adimensionais.
A que altitude h acima do pólo norte o peso de um objeto é reduzido para 10 % do seu valor na superfície terrestre? Assuma a Terra esférica com raio R e expresse h em termos de R .