Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 7.Problemas - Ex. 47

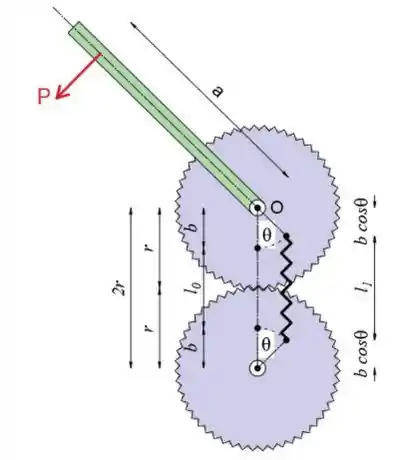
A alça é presa a uma das engrenagens conectadas por mola, que são montadas em rolamentos fixos. A mola de rigidez k conecta dois pinos montados nas faces das engrenagens. Quando a alça está na posição vertical, θ = 0 e a força da mola é zero. Determine a força P necessária para manter o equilíbrio em um ângulo θ.

Passo 1

Primeiro, vamos desenhar o diagrama de força ativa

Observe que há força P agindo no sistema, há também uma mola acoplada e que a massa é desprezada. Sabendo disso, podemos escrever a equação de equilíbrio

δ U = δ V δ U P = δ V e (1)

Podemos ver pelo esboço que o comprimento da mola não esticada é

l 0 = 2 r - 2 b

Enquanto o comprimento da mola esticada é

l 1 = 2 r - 2 b c o s ⁡ θ

Portanto, podemos escrever que a mola está esticada para

Δ l = l 1 - l 0

= 2 r - 2 b c o s ⁡ θ - ( 2 r - 2 b ) = 2 b ( 1 - c o s ⁡ θ )

Passo 2

Observe que força" P "os machos sobre o ponto" O momento de

M P = P a

Podemos escrever Trabalho Virtual pela força P como

δ U P = M P δ θ

Substituiremos   M P  por  P a

δ U P = P a δ θ (2)

Passo 3

Uma vez que rotulamos a mudança no comprimento da mola como Δl, a expressão para energia potencial elástica é

V e = 1 2 k Δ l 2

Substituiremos Δ l 2  by  4 b 2 ( 1 - c o s ⁡ θ ) 2

V e = 1 2 k ⋅ 4 b 2 ( 1 - c o s ⁡ θ ) 2 V e = 2 k ⋅ b 2 ( 1 - c o s ⁡ θ ) 2

Derivaremos ambos lados da equação

δ V e = 2 k ⋅ b 2 ⋅ 2 ( 1 - c o s ⁡ θ ) ⋅ s i n ⁡ θ δ θ (3)

substituiremos  δ U P  e  δ V e  pelas expressões (2) e (3) na equação (1)

P a δ θ = 2 k ⋅ b 2 ⋅ 2 ( 1 - c o s ⁡ θ ) ⋅ s i n ⁡ θ δ θ

Podemos expressar força P como

P = 4 k b 2 a s i n ⁡ θ ( 1 - c o s ⁡ θ )

Resposta

P = 4 k b 2 a s i n ⁡ θ ( 1 - c o s ⁡ θ )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13. A haste fina A B é presa a um colar A e repousa sobre uma pequena roda em C . Desprezando o raio da roda e o efeito do atrito, deduza uma expressão para a intensidade da força Q necessária para se
15. Uma barra uniforme A B de comprimento l e peso W é suspenso por duas cordas A C e B C de igual comprimento. Deduza uma expressão para a intensidade do binário M necessária para manter o equilíbrio
16. Deduza uma expressão para a intensidade do binário M necessária para se manter o equilíbrio do mecanismo articulado mostrado na figura.
17. Deduza uma expressão para a intensidade do binário M necessária para se manter o equilíbrio do mecanismo articulado mostrado na figura.
4. Determine o binário M que deve ser aplicado ao elemento A B C para se manter o equilíbrio do sistema articulado.