Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 14
Uma amostra para ensaio de de espessura deve ser cortada de uma placa de vinil , e submetida a uma carga de tração de . Determinar a deformação total da amostra; a deformação da mesma , na porção central.
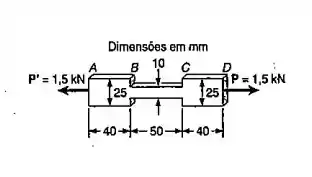
Passo 1
Opaa... Vamos pra mais uma questãozinha??
Aqui vamos usar a equação pra deformação:
Mas, como tem 3 regiões diferentes:
Então:
Passo 2
Para as áreas, a gente tem:
- para AB e CD:
- para BC:
Para os L:
- de AB e CD:
- de BC:
Para o E... Vamos só arrumar aunidade pra não dar probelam:
Passo 3
Agora vamos fazendo um por um com calmar porque precisamos achar a normal.
Para AB, o equilíbrio de forçar horizontal:
Para BC:
Para CD:
Passo 4
Jogando tudo na equação la´do passo 1:
Passo 5
b) Para a parte central a gente só pega:
Resposta
Exercícios de Livros Relacionados
Para a treliça e carregamento mostrado, determine a tensão normal na barra B D . Sabendo-se que a área da seção transversal da barra é de 1 . 290m m ² ².
Determine a menor área admissível para a seção transversal da barra D E da treliça mostrada se para o carregamento dado, a tensão normal nesta barra não deve ultrapassar 200M P a .
Para a treliça e carregamento mostrado, determine a tensão normal na barra A D . Sabe-se que a área da seção transversal da barra é de 1.200m m ² ².
Duas barras cilíndricas, uma de aço ( E = 200G P a ) e outra de latão ( E = 105G P a ), são ligadas em C e engastadas em A e E . Para o carregamento indicado, determinar: (a) as reações em A e E ; (b)
Uma barra rígida A D é sustentada, como indicado, por dois arames de aço de 1,6m m de diâmetro ( E = 200G P a ), um pino e um suporte em D . Sabendo-se que os arames estão incialmente esticados, deter