Um tubo de alumínio de de comprimento , e com diâmetro externo de e interno de , pode ser fechado em ambas as extremidades por meio de tampas com roscas simples, de de passo. Após uma das tampas ser totalmente apertada, coloca-se uma barra maciça de latão () de de diâmetro dentro deste tubo e em seguida a outra tampa é totalmente rosqueada. Como a barra é sensivelmente maior do que o tubo, observa-se que a tampa comprime a barra durante uma rotação de um quarto de volta, antes de completamente fechada. Determinar: a tensão normal no tubo e na barra; a deformação no tubo e na barra.
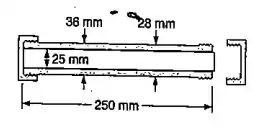
Passo 1
Fala aí galera, bora fazer mais uma questão de Resmat. Primeiramente, vamos encontrar a áreas ddo tudo de alumínio. Para a barra de alumínio, temos:
Já para a barra de latão, temos:
Com isso, podemos encontrar a deformação para cada barra, fica assim:
E para a barra de latão, temos:
E então, temos:
Logo, para encontrarmos a carga, temos que:
Substituindo:
Assim, as tensões na barra de alumínio e na barra de latão são, respectivamente:
Passo 2
Para determinarmos a deformação no tubo e na barra, temos:
Logo: