O anel aberto, com uma fenda, como mostrado, tem um raio interno e seção circular com diâmetro . Sabendo-se que cada uma das forças são aplicadas no centroide da seção transversal, determinar a tensão no ponto A; ponto B.

Passo 1

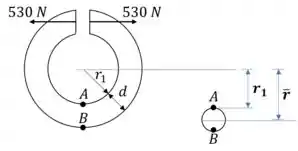
A melhor forma de começar as questões de viga curva é pelas propriedades geométricas.
Como já temos o diâmetro e o raio interno, podemos calcular o raio da seção transversal:
A área da seção:
e o raio do centroide:
o raio externo da viga:
E agora já dá pra calcular o raio da linha neutra:
Logo, a excentricidade entre o centroide e a linha neutra é:
Passo 2

Vamos fazer uma seção na região AB e calcular os esforços internos.
A força interna se equilibra com o carregamento:
E considerando que o ponto de aplicação das forças é o centroide da seção, podemos calcular o momento:
Passo 3
Agora é só calcular as tensões! Não esqueça de considerar a tensão de tração gerada pela força F
No ponto A:
No ponto B: