Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 109

Duas forças de 10 kN são aplicadas a uma barra retangular de 20 mm × 60 mm, como mostrado. Determinar a tensãono ponto A, quando: (a) b = 0; (b) b = 15 mm; (c) b = 25 mm.

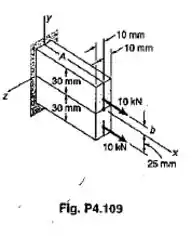
Passo 1

Vamos começar pelo Momento no eixo x (sentido horário positivo).

Σ M x = 10 × b - 10 × 25 = 10 b - 250

Temos ainda para o somatório de forças na direção x

Σ F x = 10 + 10 = 20   k N

Cálculo da área

A = b × h = 0,02 × 0,06 = 12 × 10 - 4   m 2

Podemos então calcular o σ ,   que nos será dado por

σ = F A = 20 × 10 3 12 × 10 - 4 = 16,667   M P a

Momento de inércia agora

I x = b × h 3 12 = 0,02 × 0,06 3 12 = 3,6 × 10 - 7   m 4

Passo 2

a) Com esses valores em mãos já podemos começar a resolver. Para b = 0 mm

Σ M x = 10 b - 250 = - 250   N . m

Para o σ A teremos

σ A = M c I = - 250 × 0,03 3,6 × 10 7 = - 20,833   M P a

E o σ A t o t a l   será dado por

σ A t o t a l = σ + σ A = 16,667 - 20,83 = - 4,167   M P a

Passo 3

b) Para a letra (b) teremos o mesmo passo a passo, no entanto agora com b = 15 mm

M = 10 × 15 - 25 × 10 = - 100   N . m

σ A = M c I = - 100 × 0,03 3,6 × 10 7 = - 8,3 33   M P a

E o σ A t o t a l   será dado por

σ A t o t a l = σ + σ A = 16,667 - 8,333 = 8,333   M P a

Passo 4

c) E agora com b = 25 mm

M = 10 × 2 5 - 25 × 10 = 0   N . m

Opa, pranossa sorte achamos um zerinho! Sai facilitando toda nossa vida, haha.

σ A = M c I = 0 × 0,03 3,6 × 10 7 = 0 M P a

E o σ A t o t a l   será dado por

σ A t o t a l = σ + σ A = 16,667 - 0 = 16,667   M P a

Resposta

a ) σ A t o t a l = - 4,167   M P a  

b )   σ A t o t a l = 8,333   M P a

c ) σ A t o t a l = 16,667   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga com a seção transversal mostrada está sujeita a um momento M 0 que atua em um plano vertical. Determinar o maior valor permissível do momento fletor M 0 , se a máxima tensão na viga não exced
Sabendo que uma força cortante vertical V produz a máxima tensão de cisalhamento de 75M P a no perfil cartola extrudado mostrado,determine a tensão de cisalhamento correspondente no a ponto a. b ponto
A viga construída de madeira está submetida a uma força cortante vertical de 1500i n . Sabendo que o espaçamento longitudinal dos pregos é s = 2,4i n . e que cada prego tem o comprimento de 3,5 i n .
Três placas de aço de 1x18i n . são aparafusadas a quatro cantoneiras L 6x6x1 para formar uma viga com a seção transversal mostrada. Os parafusos têm 7 8 - i n . de diâmetro e são espaçados longitudin
O projeto de uma viga requer a soldagem de quatro placas horizontais a uma placa vertical de 0.5 x 5 i n .conforme mostrado. Para uma força cortante vertical V , determine a dimensão h para a qual o f