Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 100
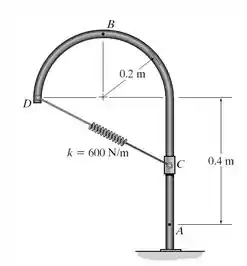
O anel de 2 kg é solto do repouso em A e desloca-se ao longo da guia vertical lisa. Determine a velocidade do anel quando ele chega à posição B. Determine também a força normal exercida sobre o anel nesta posição. A mola tem um comprimento não deformado de 200 mm .
Passo 1
Primeiramente deve-se estabeler a equação da conservação de energia cinética, energia potencial elástica e potencial gravitacional para o problema. De forma que :
(1)
Passo 2
Deve-se calcular as energias para o ponto A, de forma que a energia cinética será:
A energia potencial gravitacional será:
A energia potencial elática será:
(2)
Em (2) a deformação da mola é obtida subtraindo o comprimento não deformado da mola da distância entre as posições A e D, , de forma que:
Passo 3
Deve-se calcular as energias para o ponto B, de forma que a energia cinética será:
A energia potencial gravitacional será:
A energia potencial elática será:
(3)
Em () a deformação da mola é obtida subtraindo o comprimento não deformado da mola da distância entre as posições D e B, , de forma que:
Passo 4
Substituindo as energias encontradas em (1), temos que a única icognita será a velocidade do anel ao chegar ao ponto B, de forma que :
Passo 5
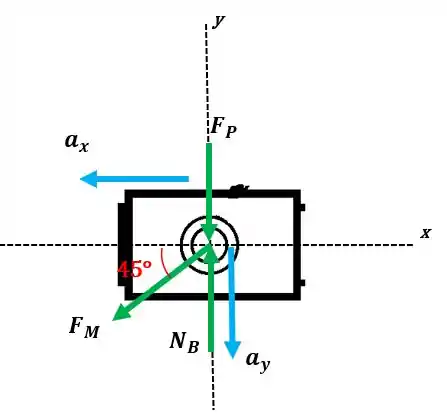
Ao chegar no ponto B o anel estará sujeito a força peso, força elática da mola e a força normal. De forma que:
Resposta
De acordo com os passos 1,2,3 e 4 a velocidade com que o anel chegará ao ponto B após ser solto da posição A, será:
E a força normal, no instante em que o anel encontra-se na posição B será:
Onde o sinal de negativo implica que a força encontra-se no sentido oposto ao adotado na resolução.