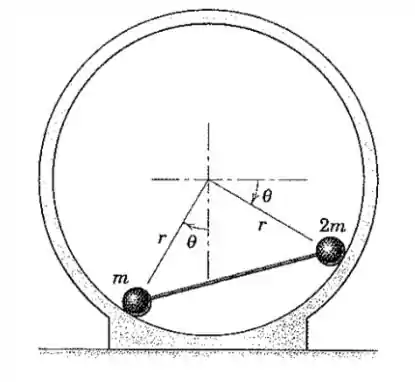
As duas partículas de massa e , respectivamente, estão conectadas por uma haste rígida de massa desprezível e deslizam com atrito desprezível em uma trajetória circular de raio no interior do anel circular vertical. Se a unidade é liberada a partir do repouso em , determine (a) a velocidade das partículas quando a haste passa a posição horizontal, (b) a velocidade máxima das partículas, e (c) o valor máximo de .

(a) Agora vamos utilizar a lei de conservação de energia:

E agora já podemos olhar para a primeira pergunta: quando a haste passa pela posição horizontal (fica paralela ao chão) ela é perpendicular à reta vertical que passa pelo centro do anel!

Olhando para a figura podemos ver que acontece quando , então:

E substituindo os valores numéricos:

(b) E agora, olhando para a fórmula, vamos tentar determinar em qual ângulo a velocidade é máxima:

Tecnicamente só queremos achar o que maximiza a velocidade, mas nesse caso podemos simplificar as coisas e simplesmente buscar o máximo de , porque o resultado será o mesmo.

E derivando em relação a :

E esse é o ângulo que maximiza a velocidade. Substituindo na fórmula de cima:

(c) Agora queremos saber o valor máximo de .

Quando a barra entra em movimento, podemos presumir que ela vai ganhar velocidade até um certo ponto de retorno e então “oscilar”. Isso quer dizer que o ponto de velocidade máxima acontece quando a energia cinética é nula:

E pela nossa fórmula:

E vamos reescrever uma das funções trigonométricas:

E elevando os dois lados ao quadrado:

E podemos chamar e resolver essa equação de grau:

E substituindo o cosseno de volta ficamos com dois ângulos possíveis:

Mas como queremos o valor máximo de :