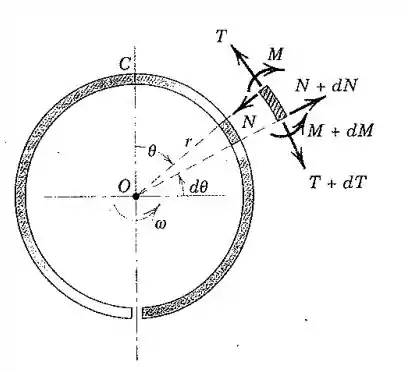
O anel de raio com uma abertura está girando em torno de um eixo vertical através do seu centro O com uma velocidade angular constante . Utilize um elemento diferencial do anel e desenvolva expressões para o esforço cortante N e a tração T no anel em termos do ângulo Determine o momento fletor no ponto C usando a metade do anel como um corpo livre. A massa do anel por unidade de comprimento de aro é
Passo 1
Bom pessoal, vamos fazer por partes. Primeiro, a figura do enunciado nos dá praticamente o diagrama de corpo livre.
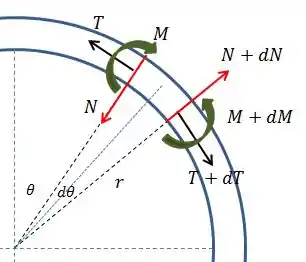
Bom, vamos aplicar a equação de equilíbrio de forças na direção radial:
onde a aceleração radial nada mais é do que a componente normal. A massa é a correspondente a este pequeno pedaço de anel . Temos ainda as componentes das forças na direção radial,
Então, expandindo a equação:
Como o ângulo é muito pequeno, podemos fazer as seguintes aproximações:
Substituindo na equação:
Reparem que o termo é muito pequeno quando comparado aos demais por ser um produto de dois números muito pequenos. Portanto, este termo pode ser desprezado. Ficamos com a seguinte equação:
Agora, vamos fazer a mesma coisa para a direção tangencial, lembrando que não há aceleração tangencial:
Derivando a primeira equação em relação a
Como a velocidade angular é constante, sua derivada é nula. Então
Substituindo na equação (2):
A solução desta EDO é dada por:
Agora devemos aplicar as condições de contorno para encontrar o valor das constantes A e B. Para , logo:
Agora, pegando a equação (1) e substituindo a expressão encontrada para N:
Vamos aplicar outra condição de contorno. Para , portanto:
Temos, então, a expressão completa para N:
Para encontrar o valor da tração T, basta usar a equação (1) novamente:
Passo 2
Para encontrar o momento no ponto C, o enunciado recomenda utilizar metade do anel.
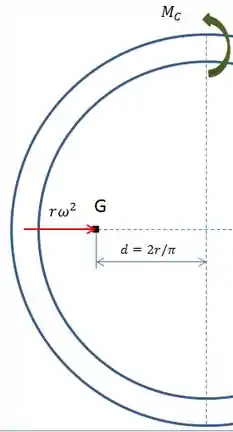
Um conhecimento importante para entender o diagrama é saber a localização do centro de massa de metade de um anel. Além disso, a aceleração normal fica concentrada neste ponto. Agora sim, podemos calcular o somatório dos momentos em C: