Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.5 - Ex. 4

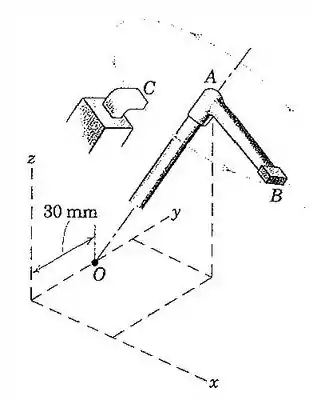
4. Um mecanismo de sincronização consiste no braço distribuidor A B que gira e no contato fixo C . Se o braço gira em torno do eixo fixo O A com uma velocidade angular constante ω → = 30 3 i ^ + 2 j ^ + 6 k ^   r a d / s , e se as coordenadas do contato C expressas em milímetros são ( 20 , 30,80 ) , determine o módulo da aceleração da extremidade B do braço distribuidor quando passa pelo ponto C   ?

Passo 1

A fórmula da aceleração para um determinado ponto do nosso sistema é dada por:

a → = ω → ˙ × r → + ω → × ( ω → × r → )

Bem! O vetor r → , nada mais é do que o valor do vetor O C → , cujas coordenadas são dadas em m m , por:

r → = O C → = 20,30,80 - 0,30,0 = 20,0 , 80   m m

E o valor do vetor velocidade angular ω → , já nos foi dado pelo enunciado. Falta agora, apenas o valor da aceleração angular ω → ˙ , que sabemos ser igual a zero, uma vez que o enunciado nos diz que o mecanismo gira com aceleração angular constante.

Como já temos tudo que precisamos, vamos logo determinar a aceleração angular a → , que sabemos com nossas descobertas anteriores, ser dada na verdade por:

a → = ω → × ( ω → × r → )

Passo 2

Primeiramente vamos determinar quanto vale ω → × r → , dado que:

r → = 10 2 i ^ + 0 j ^ + 8 k ^   m m ω → = 30 3 i ^ + 2 j ^ + 6 k ^   r a d / s

E façamos o produto vetorial com o uso da matriz para ω → × r →

ω → × r → = 300 ⋅ i ^ j ^ k ^ 3 2 6 2 0 8

ω → × r → = 300 ⋅ [ 2 ⋅ 8 - 0 ⋅ 6 i ^ - 3 ⋅ 8 - 6 ⋅ 2 j ^ + ( 3 ⋅ 0 - 2 ⋅ 2 ) k ^ ]

ω → × r → = 300 ⋅ 16 i ^ - 12 j ^ - 4 k ^   m m s

Passo 3

Obtido quanto vale ω → × r → , vamos fazer agora o produto vetorial ω → × ( ω → × r → ) , dado que:

ω → × r → = 300 ⋅ ( 16 i ^ - 12 j ^ - 4 k ^ ) ω → = 30 3 i ^ + 2 j ^ + 6 k ^   r a d / s

ω → × ω → × r → = 300 ⋅ 30 ⋅ i ^ j ^ k ^ 3 2 6 16 - 12 - 4

ω → × ω → × r → = 9000 ⋅ [ - 8 + 72 i ^ - - 12 - 96 j ^ + ( - 36 - 32 ) k ^ ]

ω → × r → = 9000 ⋅ 64 i ^ + 108 j ^ - 68 k ^   m m s 2

E como sabemos que a → = ω → × ω → × r → , então:

a → = 9000 ⋅ 64 i ^ + 108 j ^ - 68 k ^   m m s 2

a → = 576 i ^ + 972 j ^ - 612 k ^   m s 2

Bom! Nos temos o vetor a → em termo de suas componentes. Só que a questão pede o módulo da aceleração, que nós sabemos que pode ser determinado elevando as componentes do vetor ao quadrado, somando e em seguida tirando a raiz:

a = ( 576   m / s ) 2 + ( 972   m / s ) 2 + ( - 612   m / s ) 2

a = 1651104   m / s

a ≅ 1285   m / s

Resposta

M ó d u l o   d a   a c e l e r a ç ã o → a ≅ 1285   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se um disco rola sem deslizar sobre uma superfície horizontal, mostre que quando os momentos são somados em relação ao centro instantâneo de velocidade nula, CI, é possível usar a equação de momento ∑
A tábua de 25 kg está suspensa pelas cordas em C e D. Se essas cordas estão submetidas a forças constantes de 150 N e 225 N, respectivamente, determine a aceleração inicial do centro da tábua e sua ac
A bobina tem uma massa de 100 kg e um raio de giração k G = 0,3m . Se os coeficientes de atrito cinético e estático em A são μ s = 0,2 e μ k = 0,15 , respectivamente, determine a aceleração angular da
O disco semicircular tendo uma massa de 10 kg está girando a ω = 4r a d / s no instante θ = 60 ° . Se o coeficiente de atrito estático em A é μ s = 0,5 , determine se o disco desliza neste instante.
O rolo de grama tem uma massa de 80 kg e um raio de giração k G = 0,175m . Se ele for empurrado para frente com uma força de 200 N quando o punho está a 45°, determine sua aceleração angular. Os coefi