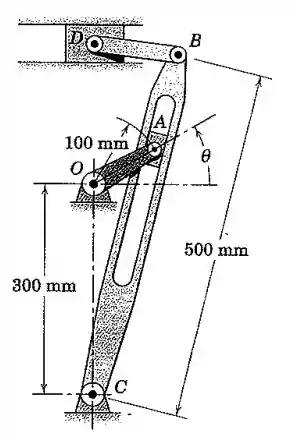
A figura ilustra um mecanismo de retorno rápido, comumente utilizado, que realiza um movimento lento de corte da ferramenta (presa em D) e um movimento rápido de retorno. Se a manivela de acionamento AO está girando na taxa constante de , determine o módulo da velocidade do ponto B para o instante em que

Bom pessoal, vamos supor um ponto P coincidente a A, mas que pertence ao elemento ranhurado BC. Desta forma, temos que a velocidade do ponto P é perpendicular a BC, assim como a velocidade de A é perpendicular a manivela AO. Além do mais, o cursor A só pode se movimentar pela ranhura, o que faz com que a velocidade relativa esteja nesta direção. Vamos fazer um esboço do mecanismo com os vetores velocidade.

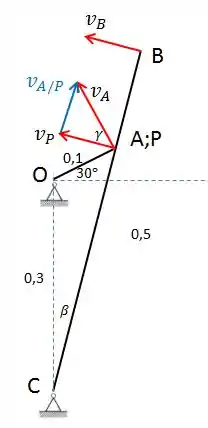
Podemos calcular a distancia CA pela lei dos cossenos no triângulo AOC:

O ângulo beta pode ser obtido pela lei dos senos:

A velocidade de A pode ser obtida a partir da manivela AO:

Como sabemos o vetor posição de P, podemos então achar uma relação para sua velocidade:

E a velocidade relativa entre A e P sabemos que está na direção da ranhura:

Agora, basta usarmos a equação da velocidade relativa:

Substituindo os valores:

Decompondo nas direções i e j:

Resolvendo o sistema, temos que:

Com isso, podemos calcular a velocidade de B: