Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 76

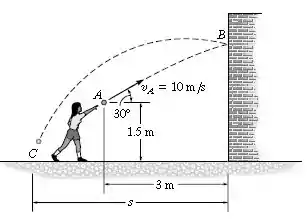
A garota lança a bola de 0,5   k g na direção da parede, a uma velocidade inicial de v A = 10   m / s . Determine: (a) a velocidade com que a bola atinge a parede em B ; (b) a velocidade com a qual ela quica na parede se o coeficiente de restituição for e = 0,5 ; e (c) a distância s , da parede até onde ela atinge o solo em C .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Considerando o movimento horizontal da bola antes do impacto, temos:

s x = s 0 x + v x t

3 = 0 + 10 cos ⁡ 30 ° t

t = 0,3464   s

Analisando agora o movimento vertical:

v y = v 0 y + a y t

v y = 10 sin ⁡ 30 ° + ( - 9,81 ) ( 0,3464 )

v y = 1,602   m / s

A altura do ponto B é dado por:

s y = s 0 y + v 0 y t + 1 2 a y t 2

s B y = 1,5 + 10 sin ⁡ 30 ° 0,3464 + 1 2 - 9,81 0,3464 2

s B y = 2,643   m

A magnitude da velocidade e a direção são dadas por:

v b 1 = 10 cos ⁡ 30 ° 2 + 1,602 2

v b 1 = 8,807   m / s

θ = tan - 1 ⁡ 1,602 10 cos ⁡ 30 °

θ = 10,48 °

Passo 2

Vamos aplicar o principio da conservação de quantidade de movimento para quando a bola atinge a parede com uma velocidade v b 1 e sai com uma velocidade v b 2 .

m b v b y 1 = m b v b y 2

m b ( 1,602 ) = m b v b 2 sin ⁡ ϕ

Onde ϕ , é o ângulo de saída que a bola faz ao bater no muro.

v B 2 sin ⁡ ϕ = 1,602

Precisamos de outra equação para resolver o sistema, temos:

0,5 = 0 - - v b 2 cos ⁡ ϕ 10 cos ⁡ 30 ° - 0

v b 2 cos ⁡ ϕ = 4,33

Relacionando as equações e resolvendo o sistema, temos:

v B 2 sin ⁡ ϕ v b 2 cos ⁡ ϕ = 1,602 4,33

tan ⁡ ϕ = 1,602 4,33

ϕ = tan - 1 ⁡ 1,602 4,33

ϕ = 20,3 °

Logo:

v B 2 sin ⁡ 20,3 ° = 1,602

v b 2 = 4,62   m / s

Passo 3

Agora vamos analisar o movimento vertical e horizontal após o impacto:

s y = s 0 y + v 0 y t + 1 2 a y t 2

- 2,643 = 0 + 4,617 sin ⁡ 20,3 ° t 1 + 1 2 - 9,81 t 1 2

t 1 = 0,9153   s

s x = s 0 x + v x t

S = 0 + 4,617 cos ⁡ 20,3 ° ( 0,9153 )

S = 3,96   m

Resposta

a )   v b 1 = 8,807   m / s

θ = 10,48 °

b ) v b 2 = 4,62   m / s

ϕ = 20,3 °

c ) S = 3,96   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um painel de madeira de 8 kg é suspenso por um pino suporte em A e está inicialmente em repouso. Uma esfera de metal de 2 kg é liberada do repouso em B e cai dentro de uma concha semiesférica C presa
Uma barra delgada uniforme AB de massa m está em repouso sobre uma superfície horizontal sem atrito quando o gancho C engata em um pequeno pino em A. Sabendo que o gancho é puxado para cima com uma ve
Uma barra delgada uniforme de comprimento L e massa m é apoiada por uma mesa horizontal sem atrito. Inicialmente, a barra está girando em torno de seu centro de massa G com uma velocidade angular cons
Um painel de madeira de 8 kg é suspenso por um pino suporte em A e está inicialmente em repouso. Uma esfera de metal de 2 kg é liberada do repouso em B’ e cai dentro de uma concha semiesférica C’ pres
Uma barra delgada uniforme de comprimento L cai contra suportes rígidos em A e B. Como o suporte B está ligeiramente abaixo do suporte A, a barra bate no suporte A com uma velocidade v - 1 antes de ba