Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 109
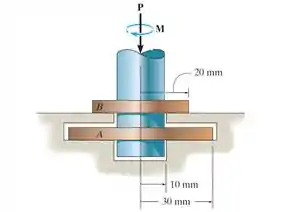
O mancal de dupla escora está sujeito a uma força axial . Supondo que a escora A suporte e a escora suporte , ambas com uma distribuição uniforme de pressão, determine o maior momento de atrito que pode ser resistido pelo mancal. Considere para as duas escoras.
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Temos que calcular o maior momento de atrito que pode ser resistido pelo mancal de escora.
Mas, antes de nos preocuparmos com a questão de ter duas escoras, vamos comemorar um pouco. Para a nossa alegria, a fórmula que relaciona o torque com este coeficiente de atrito já foi desenvolvida na seção 8.6! Então, temos apenas que aplicar a fórmula aqui.
Sendo assim, temos:
Agora que já sabemos a relação base, basta sabermos como trabalhar com a dupla escora. E é muito simples! Basta somarmos o efeito do momento relativo à escora A e a escora B. E aí a gente considera a força relativa para cada escora.
Sendo assim, o momento será:
E assim finalizamos a questão!