Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 99
99. Resolva o problema incluindo o efeito de um coeficiente de resistência ao rolamento de .
Passo 1
Bom! Antes de mais nada, a primeira coisa que temos que fazer é o esboço de uma das rodas do vagão ferroviário. Olho lá, que como são oito rodas, o peso total vai ser dividido por .
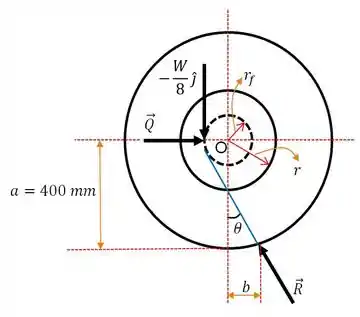
Olha que belezinha de imagem, né não? Vamos logo pro que interessa.
A distância perpendicular entre o centro da roda e a linha de ação de , de problemas anteriores, já sabemos que é dada por:
Agora, pense só o seguinte!! Nesses casos o ângulo com o qual estamos trabalhando é muito, mas muito pequeno. O que acontece com o seno e o cosseno do ângulo nessas condições?
Bom! Se temos essas relações acima, consequentemente obtemos que:
E da bela figurinha que construímos anteriormente, tiramos que:
Passo 2
A próxima coisa que temos que fazer, é o triângulo de forças, com as três forças que temos na figura:
E disso, tiramos que:
Só que:
O que nos leva à:
Essa é a expressão que obtemos para apenas uma roda. Lembre-se bem que são oito rodas presentes no vagão. Chamando a força total que queremos obter de , temos então que ela é dado por vezes :
Onde já sabemos os seguintes valores:
Passo 3
a) Para essa letra, o valor de é dado por . Logo, para encontrar nossa resposta, basta usar a fórmula:
Passo 4
b) Já para essa letra, o valor de é dado por . Logo, para encontrar nossa resposta, basta usar a fórmula:
Resposta
a)
b)