Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 208
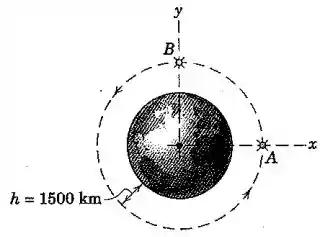
Os satélites e estão em uma órbita circular de altitude . Determine o módulo da aceleração do satélite em relação a um observador sem rotação no satélite . Utilize para a aceleração gravitacional no nível da superfície e para o raio da Terra.
Passo 1
Galera, vamos recordar que a aceleração gravitacional numa altura é dada por:
Cada satélite terá aceleração apontando para o centro da Terra, então:
Passo 2
A aceleração relativa do satélite vista por um observador no satélite pode ser dada por:
Dessa forma, o módulo da aceleração relativa será:
Resposta
Exercícios de Livros Relacionados
No instante mostrado, os carros A e B movem-se a velocidades escalares de 70 km/h e 50 km/h, respectivamente. Se B está aumentando a sua velocidade na razão de 1100 Km/h2 , enquanto A mantém uma veloc
Um carro está se deslocando na direção norte ao longo de uma estrada reta a 50 km/h. Um instrumento no carro indica que o vento está direcionado para leste. Se a velocidade escalar do carro é 80 km/h,
Um porta-aviões está se deslocando para a frente com a velocidade de 50 km/h. No instante mostrado, o avião em A decolou e alcançou uma velocidade escalar e horizontal para a frente no ar de 200 km/h,
Dois barcos deixam a margem ao mesmo tempo e movem-se nas direções mostradas. Se V A = 6 m/s e V B = 4,5 m/s. Determine a velocidade do barco A em relação ao barco B. Quanto tempo depois de terem deix
No instante mostrado, os carros A e B movem-se a velocidade escalares de 30 km/ h e 20 km/h, respectivamente. Se A está aumentando a sua velocidade escalar na razão de 400 km/h2 enquanto a sua velocid