Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 207

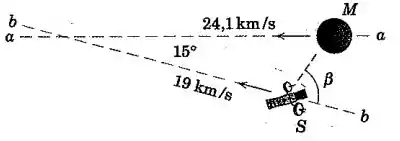
A nave espacial S aproxima-se do planeta Marte ao longo de uma trajetória b - b no plano orbital de Marte com uma velocidade absoluta de 19   k m / s . Marte tem uma velocidade de 24,1   k m / s ao longo de sua trajetória a - a . Determine o ângulo β entre a linha de visada S - M e a trajetória b - b quando Marte aparenta, a partir da nave espacial, estar se aproximando diretamente.

Passo 1

O mais importante a se notar aqui é que Marte vai aparentar estar se aproximando diretamente da nave espacial quando a velocidade relativa v M S estiver apontando na direção da linha de visada S - M .

A partir de agora, só nos resta aplicar a geometria, pois as velocidades como representadas na figura seguem as mesmas proporções que os lados correspondentes do triângulo pontilhado.

Então, aplicando a Lei dos Cossenos, temos:

v M S 2 = v M 2 + v S 2 - 2 v M v S cos ⁡ 15 °

v M S 2 = 24,1 2 + 19 2 - 2 24,1 19 cos ⁡ 15 °

v M S 2 = 57,22

v M S = 7,56   k m / s

Passo 2

Show! Agora vamos aplicar a Lei dos Senos:

v S M s e n   15 ° = v M s e n 180 ° - β

7,56 s e n   15 ° = 24,1 s e n 180 ° - β

s e n 180 ° - β = 0,8251

Porém, lembre-se de que s e n 180 ° - β = s e n   β :

s e n   β = 0,8251

β = s e n - 1 0,8251

β = 55,6 °

Resposta

β = 55,6 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um homem caminha a 5 km/h na direção de um vento de 20 km/h. Se gotas de chuva caem verticalmente a 7 km/h no ar parado, determine a direção na qual as gotas parecem cair em relação ao homem suponha q
Um homem pode remar um barco a 5 m/s na água parada. Ele quer atravessar um rio de 50 m de largura até o ponto B, 50 m correnteza abaixo. Se o rio flui com uma velocidade de 2 m/s, determine a velocid
Dois ciclistas A e B movem-se com a mesma velocidade escalar constante de v. Determine a velocidade de A em relação a B se A se desloca ao longo da pista circular. Enquanto B se desloca ao longo do di
No instante mostrado, o carro A está se deslocando com uma velocidade de 30 m/s e tem uma aceleração de 2 m/s2 ao longo da autoestrada. No mesmo instante, B está se deslocando na curva do trevo rodovi
O movimento do anel em A é controlado por um motor em B de tal maneira que quando o anel está em s A = 3 m ele está se desacelerando a razão de 1 m/ s 2 . Determine a velocidade e aceleração de um pon