Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.8 - Ex. 206

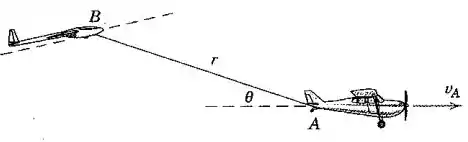
O avião A está voando horizontalmente com uma velocidade constante de 200   k m / h e está rebocando o planador B , que está ganhando altitude. Se o cabo de reboque tem um comprimento r = 60   m e θ está aumentando na taxa constante de 5 graus por segundo, determine os módulos da velocidade v e da aceleração a do planador para o instante em que θ = 15 ° .

Passo 1

Pessoal, pra descobrir o módulo da velocidade v de B , vamos usar a seguinte relação:

v = v A + v B A

onde v B A é a velocidade relativa de B em relação a A . Para o avião A , parece que o planador está apenas girando através da corda com velocidade constante, dada por:

v B A = r θ ˙ = 60 5 π 180 = 5,24   m / s

onde convertemos a taxa θ ˙ de graus por segundo para radianos por segundo.

Essa velocidade relativa, por ser perpendicular à corda (movimento circular), faz com a horizontal um ângulo α = 90 ° - θ , de modo que podemos decompor essa velocidade nos eixos x e y assim:

v B A = 5,24   cos ⁡ α i + 5,24   s e n   α   j

v B A = 5,24   s e n   θ   i + 5,24 cos ⁡ θ j

Usando θ = 15 ° , obtemos:

v B A = 1,36   i + 5,06   j

Passo 2

Sabemos que v A = 200   k m / h = 55,56   m / s . Escrevendo isso vetorialmente:

v A = 55,56   i + 0   j

Portanto, usando a relação citada no início, obtemos:

v = v A + v B A = 55,56   i + 0   j + 1,36   i + 5,06   j

v = 56,92   i + 5,06   j

Podemos então calcular o módulo de v :

v = 56,92 2 + 5,06 2

v = 57,1   m / s

Passo 3

Para calcular o módulo da aceleração a , usamos uma relação bastante parecida:

a = a A + a B A

Mas agora temos a A = 0 , pois o avião A se move com velocidade constante. Então:

a = a B A

E portanto, em módulo:

a = a B A

A aceleração a B A é devido ao movimento circular, então ela será dada pela fórmula da aceleração normal:

a n = v 2 r

a = v B A 2 r

Temos r = 60   m e v B A = 5,24   m / s , como calculado no P a s s o   1 :

a = 5,24 2 60

a = 0,46   m / s 2

Resposta

v = 57,1   m / s

a = 0,46   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O navio move-se com uma velocidade escalar constante vs = 20 m/s e o vento está soprando a uma velocidade escalar vW = 10 m/s, como mostrado. Determine a intensidade e direção da componente horizontal
No instante mostrado, os carros A e B movem-se a velocidades escalares de 30 km/h e 20 km/h, respectivamente. Se B está aumentando a sua velocidade escalar na razão de 1200 km/h2, enquanto A mantém um
O carro B está se deslocando ao longo da estrada curva com uma velocidade escalar de 15 m/s enquanto reduz sua velocidade escalar 2 m/s2. Nesse mesmo instante, o carro C está se deslocando ao longo da
O carro A move-se ao longo de uma estrada reta com uma velocidade escalar de 25 m/s acelerando a 1,5 m/s2. Nesse mesmo instante, o carro C está se deslocando ao longo da estrada reta com uma velocidad
No instante mostrado, os carros A e B movem-se a velocidade de 70 Km/h e 50 Km/h, respectivamente. Se B está reduzindo sua velocidade escalar na razão de 1400 km/h2, determine a aceleração de B em rel