Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 83
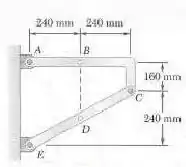
Determine os componentes das reações em e quando uma força de direcionada verticalmente para baixo é aplicada em , em .
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Desenhe o diagrama de corpo livre do quadro:
Passo 2
Vamos fazer o somatório dos momentos no ponto :
Fazendo agora o somatório das forças na horizontal, temos:
Fazendo somatório das forças na vertical, temos:
Passo 3
Agora vamos às análises internas. Temos que:
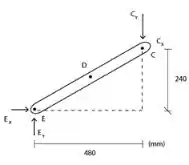
A partir do aspecto construtivo podemos dizer que:
Como , teremos que:
Portanto:
Passo 4
Item b):
Para o item b, temos que:
Agora, vamos fazer o somatório no diagrama para calcular a reação em :
Resposta
Exercícios de Livros Relacionados
Determine a força desenvolvida em cada membro da treliça espacial e indique se os membros estão sob tração ou compressão. A caixa possui um peso de 750N .
Determine a força nos membros F E e E D da treliça espacial e indique se os membros estão sob tração ou compressão. A treliça é sustentada por juntas esféricas em C e ligações curtas em A e B .
Determine a força nos membros B E , D F e B C da treliça espacial e indique se os membros estão sob tração ou compressão.
Determine a força nos membros A B , A E , B C , B F , B D e B E da treliça de espaço e indique se os membros estão sob tração ou compressão.
Determine a força nos membros A B , C D , E D e C F da treliça espacial e indique se os membros estão sob tração ou compressão.